WAVE PACKETS

Wave Packets
A wave packet refers to the case where two (or more) waves exist simultaneously. A wave packet is often referred to as a wave group.
This situation is permitted by the principle of superposition. This principle states that if any two waves are a solution to the wave equation then the sum of the waves is also a solution. This principle holds only for linear systems.
Here we consider linear, one-dimensional sinusoidal disturbances. The first figure shows an example.
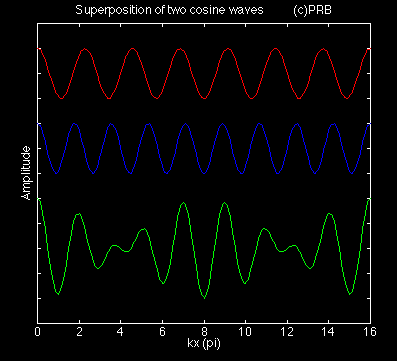
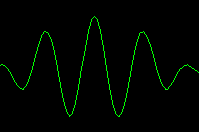
The red curve displays a simple wave form. The blue curve is another wave with a different wavelength. The wavelength is defined as the horizontal distance between two crests or between two troughs. (A crest corresponds to a wave maximum; a trough to a wave minimum.) The wavelength of the red wave is longer than that of the blue wave.
The amplitude of the two waves is the same. Here the amplitude corresponds to the half the vertical distance between the crest and the trough. The amplitude of each wave equals the distance between the vertical tic marks in the diagram.
The green curve shows the sum of the two waves. It is the wave packet.
The amplitude of the packet is twice the amplitude of either the red or the blue wave. The crests and the troughs of either the red or blue wave have the same value anywhere along the wave. For the wave packet the value of the crest and the trough varies along the wave. This variation is a result of interference between the two waves. Recall that the packet is the sum of the two waves. At certain locations the two waves have a crest at the same point so the crest of the wave packet is twice the individual wave crest. This situation is called constructive interference since the two wave amplitudes add together. Constructive interference is also visible when the two wave troughs coincide. When a wave trough and a wave crest coincide, then the wave packet is zero. This situation is called destructive interference. A node or point of zero amplitude exists where there is complete destructive interference.
The wave packet can also be thought of as the product of two waves.
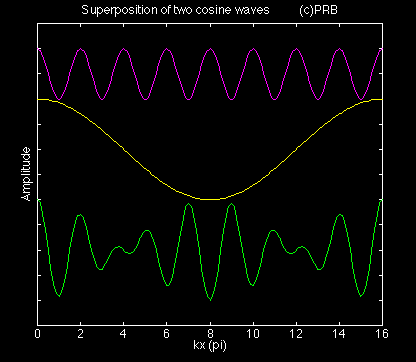
The top purple curve is called the average wave. It has the same amplitude as either the red or blue curve but its wavelength is the average of that of the red and blue wave. Count the number of crests in each of the waves and confirm this statement.
The average wave is also called the carrier wave.
The middle yellow curve is the wave envelope. It has an amplitude twice that of either the individual wave but its wavelength is half the difference of the red and the blue wave. The wavelength associated with the wave envelope is much larger than that of the carrier wave. The wave envelope is also called the wave modulation or wave amplitude.
The product of the carrier wave and the wave envelope appears as the bottom green curve. It is the same as the wave packet.
Motion of a Wave Packet
Our discussion so far holds for any pair of linear waves. The evolution of the wave packet depends on the type of wave. View these movies to examine the variety of ways a wave packet can evolve with time. Caution: The size of each mpeg movie is about 512k bytes.
Each movie shows the red and the blue waves, the packet as a solid green curve while the wave envelope (and its negative) is shown as a dashed yellow curve.
Case A displays right moving waves with the same phase velocity. Note that the wave packet moves at the same speed as the red and blue waves. The wave packet does not change shape with time. These waves are nondispersive.
Click to download the MPEG movie Case A.
Case B is identical to Case A but the waves propagate to the left. To view Case B run Case A backwards in time.
Light, sound waves, and shallow water waters are nondispersive and behave like cases A and B.
Case C displays right moving waves for which the long wavelength red wave travels slower than the blue wave. These waves are dispersive. The wave envelope travels more slowly than the carrier wave.
Click to download the MPEG movie Case C.
Case D is identical to Case C but the waves propagate to the left. To view Case D run Case C backwards in time.
Deep water gravity waves and internal gravity waves are dispersive and behave like cases C and D.
Case E shows the red and blue waves propagating to the left while the wave envelope moves to the right.
Click to download the MPEG movie Case E.
Case F shows left moving waves whose wave envelope is stationary.
Click to download the MPEG movie Case F.
Rossby waves are dispersive waves that behave like Cases D, E, or F. Since all Rossby waves propagate to the west, we must assume that west is to the left in the diagrams.
So far we have only considered waves of equal amplitude. Case G repeats case A but for the long wave having half the amplitude of the blue wave.
Click to download the MPEG movie Case G.
Credits: Inspiration for these wave movies came from:
Crawdord, F. S., Jr., Waves. New York, McGraw-HIll, 600 pp.
Dutton, J. A., Dynamics of Atmospheric Motion. New York, Dover, 617 pp.
Raymond Shaw developed the initial source code. Andy Jacobson helped with the final format and the conversion to mpeg files.
Two dimensional internal gravity waves for which the group velocity is at right angles to the phase velocity!
Send any suggestions, comments, or problems to
Last Updated: April 22, 1996