Sulfur dioxide / water equilibrium

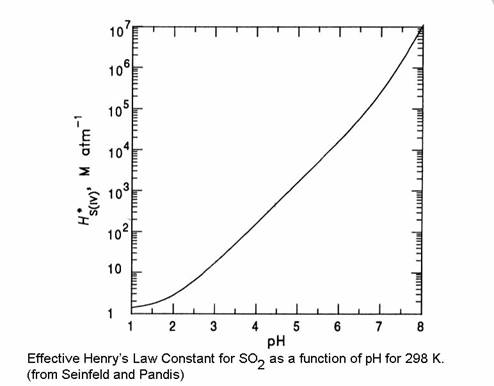
Note that H*_S(IV) is always greater than H_S(IV). Note also that the total dissolved sulfur is dependent on the pH.

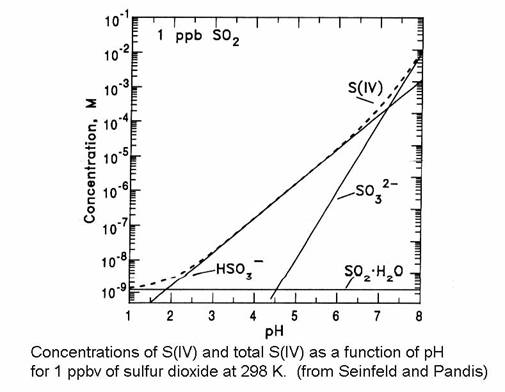
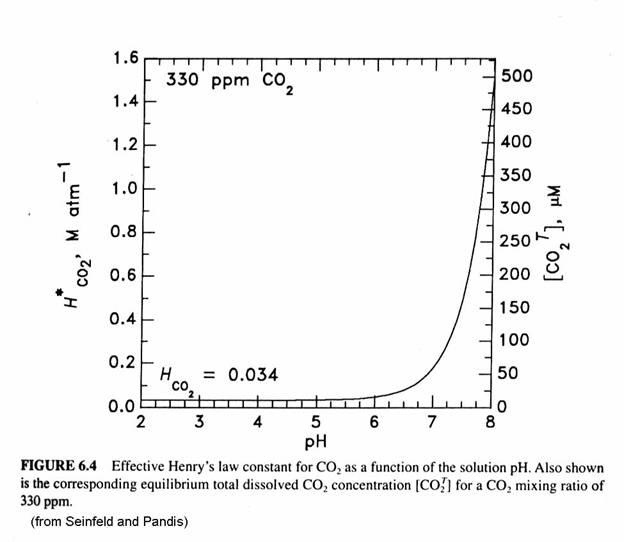
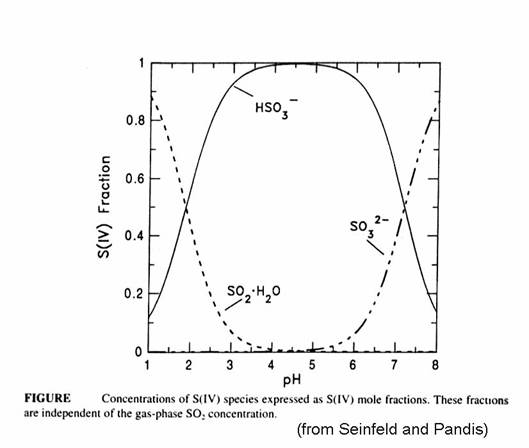
The fraction of S(IV) that is SO₂∙H₂O, HSO₃^-, and SO₃^2- is given in the next figure. Note that the bisulfite ion is the most important for much of the range of cloud water. Recall that atmospheric CO₂ creates cloud water with a pH of 5.6. The form of the sulfur becomes quite important when we think about reactions of sulfur compounds in the aqueous phase.

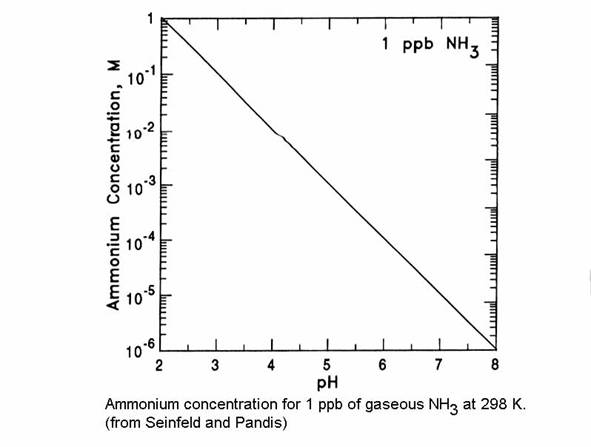
Ammonia /water equilibrium.

Nitric acid / water equilibrium.

List of constants.

The following table contains the Henry’s Law Constants and the Equilibrium Constants for the atmospheric constituents and equilibria discussed above. These equilibria are temperature dependent, but we will assume that the temperature is always near 298 K. for our discussions.

Selected Henry’s Law Constants and Equilibrium Constants at 298 K.
Equilibrium	H (mole L^-1 atm^-1)	K (M)
H2O ↔ H^+ + OH^-		1.0 x 10^-14
CO2 + H2O ↔ CO2∙H2O	3.4 x 10^-2
CO2∙H2O ↔ H^+ + HCO3^-		4.3 x 10^-7
HCO3^- ↔ H^+ + CO3^2-		4.7 x 10^-11
SO2 + H2O ↔ SO2∙H2O	1.23
SO2∙H2O ↔ H^+ + HSO3^-		1.32 x 10^-2
HSO3^- ↔ H^+ + SO3^2-		6.42 x 10^-8
NH3 + H2O ↔ NH3∙H2O	62
NH3∙H2O ↔ NH4^+ + OH^-		1.8 x 10^-5
HNO3 + H2O ↔ HNO3∙H2O	2.1 x 10^5
HNO3∙H2O ↔ H^+ + NO3^-		15.4
H2O2 + H2O ↔ H2O2∙H2O	7.45 x 10^4
H2O2∙H2O ↔ H^+ + HO2^-		2.5 x 10^-12
O3 + H2O ↔ O3∙H2O	0.011

Aqueous sulfur chemistry

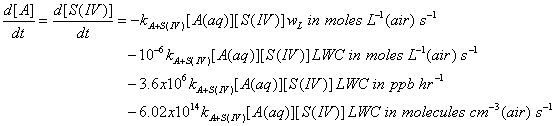
The reaction rate coefficient should have units of L mole^-1 s^-1; the concentrations are M = moles L(aq)^-1; LWC is g m^-3; and w_L is (moles L(aq)^-1)/(moles L(g)^-1).

If we want to express these equations in terms of per cent change per hour, we simply divide the third expression by the mixing ratio of SO₂ and multiply by 100:

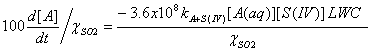
The lifetime is simply this 100 divided by this last equation, in units of hours.

We can also get the fraction converted per unit time. The fraction of sulfur converted per unit time is the conversion rate divided by the total amount of sulfur not yet converted, in both the gas and the liquid phase. The fractional rate is thus:

fraction converted per unit time = {d([S(IV)])/dt} / {p_SO2/RT + H*_SO2 p_SO2 w_L}

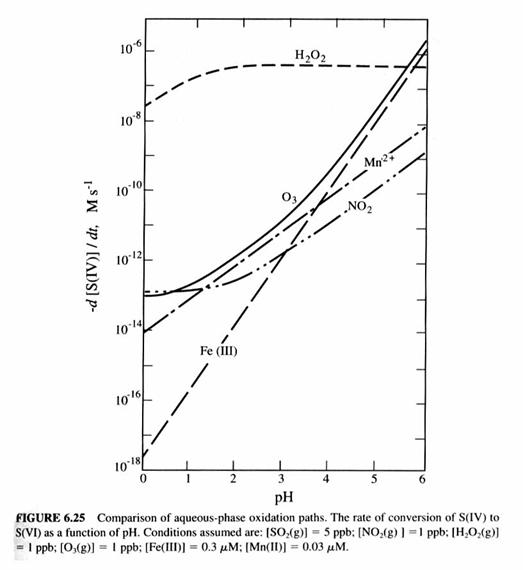
Now let’s look specifically at the oxidation of S(IV) to S(VI). We can see the reaction rates for typical amounts of different oxidants. The liquid-phase oxidants, H₂O₂ and O₃, are largely created in the gas-phase and absorbed into the liquid. Note that O₃ and H₂O₂ are both formed by processes involving HO_x radicals. We should expect that the greatest oxidation will occur during the day, when oxidant concentrations are largest, and will be greater in the summer than the winter for the same reason.

Open and closed systems.

1. Open system.

1. Gas partial pressures are maintained at fixed values by resupply from new air or from photochemistry.

2. Not a very realistic condition.

2. Closed system.

1. gas-phase partial pressures decrease with time.
2. More representative of actual behavior.
3. Masses of elements, such as S, N, C are conserved in the process.

Let us consider what happens in a closed system.

In an open system, [H₂O₂(aq)] = H_H2O2 p⁰_H2O2. In this case, the aqueous phase H₂O₂ is independent of LWC.

In a closed system, initial H₂O₂ is split between the gas and aqueous phases, as the cloud forms:

[H₂O₂]_total = (p_H2O2/RT) + [H₂O₂(aq)]_closed w_L

where recall that w_L has units of L liquid / L air and R = 0.082 (atm L)/(mole K).

If we are in equilibrium, then Henry’s Law holds and:

[H₂O₂(aq)]_closed = H_H2O2 p_H2O2

If initially there was no cloud, then the conservation equation for H₂O₂ becomes:

p^o_H2O2 = p_H2O2 + [H₂O₂(aq)]_closed w_L RT

= [H₂O₂(aq)] {(1/H_H2O2) +w_L RT}

Combining these equations, we get:

[H₂O₂(aq)]_closed = (H_H2O2 p^o_H2O2) / (1 + H_H2O2 w_L RT)

Note that [H₂O₂(aq)] decreases as LWC or w_L increases. More water means that more H₂O₂ can be accommodated in the aqueous phase. The open system is represented by the dashed lines. For the closed system, because p_H2O2 is proportional to [H₂O₂(aq)], p_H2O2 drops as [H₂O₂(aq)] drops. In addition, because p_H2O2 is proportional to [H₂O₂(aq)], the fraction of H₂O₂ that is in the aqeuous form [H₂O₂(aq)] increases as the LWC increases.

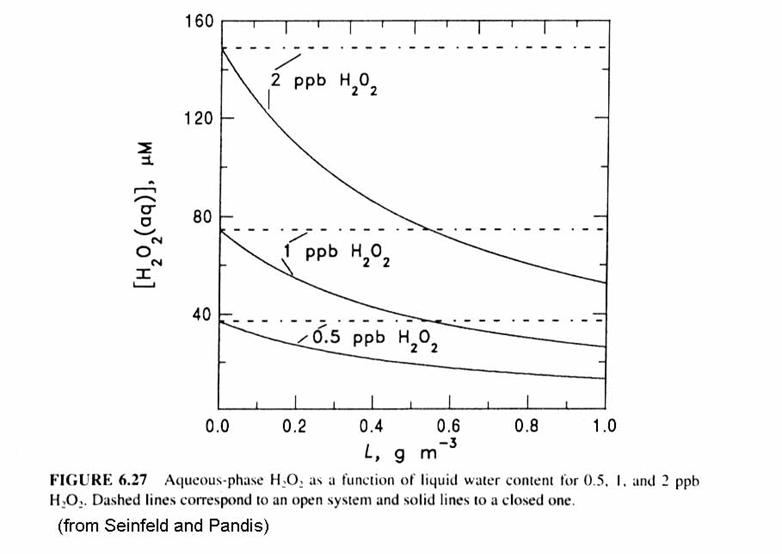
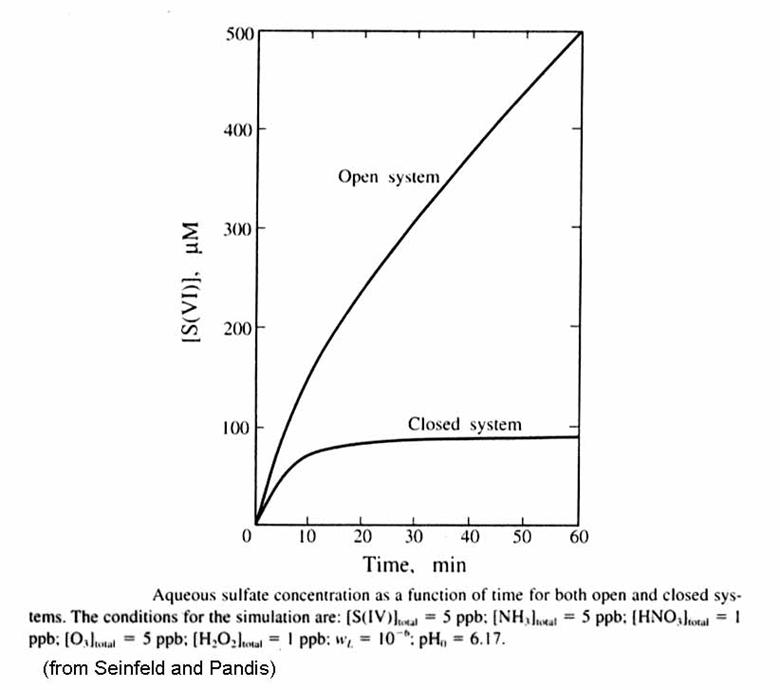
More sulfate is produced in the open system than the closed system, as in the figure below. This makes sense: the oxidants and SO₂ are being constantly replaced and is thus able to continue the conversion of S(IV) to S(VI).

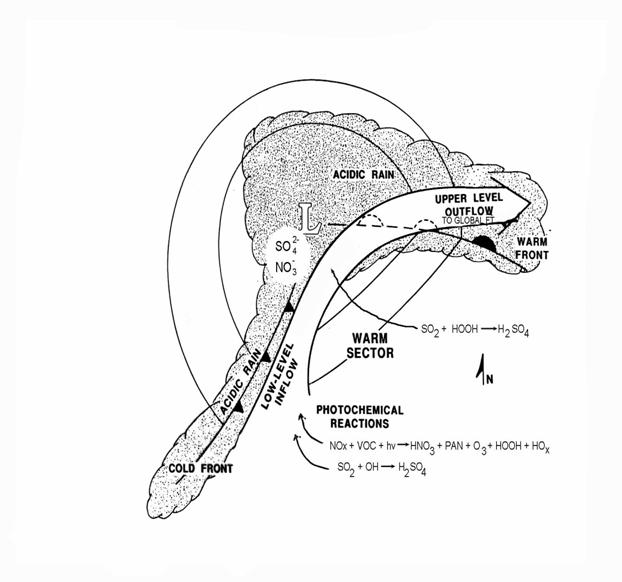
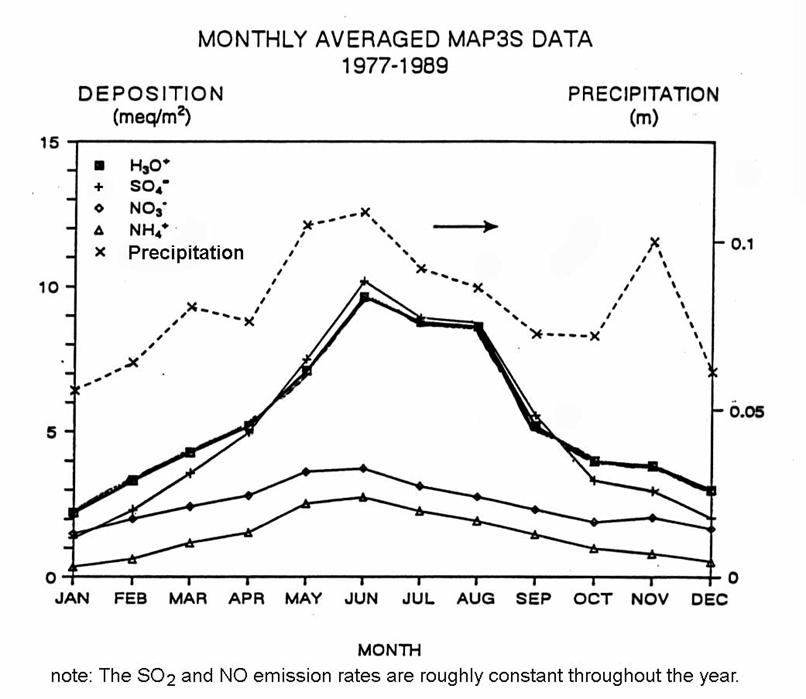
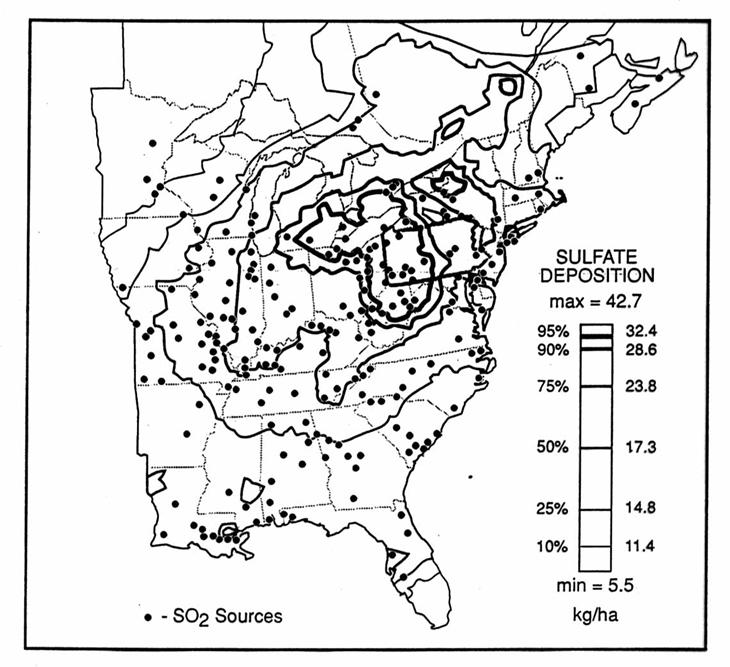
The pattern of sulfate deposition for the Eastern United States is shown in the following figure.

The figure below shows the annual variation of deposition for sites in the Eastern United States. There is a clear peak in deposition during the summer months. This peak is not due to increases in SO₂ and NO emissions, which are roughly constant over the whole year. What could be the cause of this summertime increase?