5. Aqueous phase chemistry

Because the heterogeneous processes described in Chapter 4 are so fast, we can consider aqueous chemistry to be equilibrium chemistry for periods longer than a few seconds. Recall that the development and dissipation of clouds is typically tens of minutes, and sometimes more. So equilibrium aqueous chemistry should be very applicable to issues such as acid rain.

5.1 Aqueous-phase equilibria

In the aqueous phase, several chemical species rapidly dissociate into ions. The time constant achieving equilibrium between the adsorbed gas and its ions in solution is typically less than 1 ms. Thus, we can assume equilibrium for our calculations.

5.1.1 Water.

Water ionizes in to the hydrogen ion, H⁺, and the hydroxide ion, OH^-. In reality, H⁺ quickly attaches to another water to form the hydronium ion, H₃O⁺.

At equilibrium, H₂O Û H⁺ + OH^- (or H₂O + H₂O Û H₃O⁺ + OH^-1)

K_w^’ = 1.82 x 10^-16 M at 298 K. But [H₂O] = 55.5 M = 55.5 mole/L, which is much larger than the concentration of the ions and is essentially constant. We multiply by [H₂O] to get the ion product of water: K_w’[H₂O]

K_w = 1.0 x 10^‑14 M² at 298 K. In pure water, [H⁺] = [OH^‑].

The pH of water is defined as pH = - log₁₀[H⁺], and is 7.0 at 298 K. When pH is less than 7, the solution is acidic. When pH is greater than 7, the solution is basic.

5.1.2. Carbon Dioxide / Water Equilibrium.

CO₂ hydrolyzes in water to form CO₂·H₂O, which is sometimes called CO₂(aq). The following equilibria are established:

CO₂(g) + H₂O Û CO₂·H₂O

CO₂·H₂O Û H⁺ + HCO₃^- (bicarbonate ion) K_c1

HCO₃^- Û H⁺ + CO₃^2- (carbonate ion) K_c2

Now that we have the equations, we can set up the equilibria. and then solve the simultaneous equations:

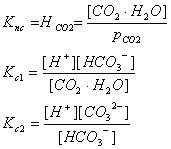
We want to get all of these in terms of things that we can actually measure.

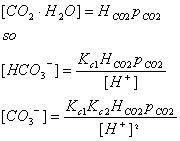
We are interested in several quantities, including the total dissolved carbon:

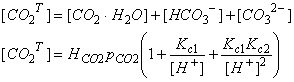
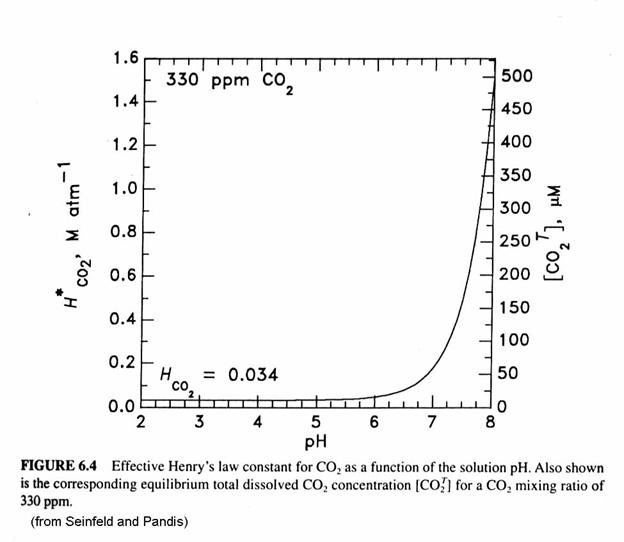
More carbon is dissolved than we would expect from Henry’s Law alone. We can determine an effective Henry’s Law constant, which will be greater than the actual Henry Law Constant:

Note that the effective Henry’s Law Constant is greater than the Henry’s Law Constant. This difference results from the carbon that is dissolved in forms other than [CO₂∙H₂O], which is in equilibrium with the gas-phase CO₂. We see that the effective Henry’s Law constant is dependent on pH through the hydronium ion concentration, [H⁺] = [H₃O⁺], as can be seen in following figure. The total amount of dissolved carbon is a strong function of pH, or [H⁺]. The effective Henry’s Law Constant for a pH of 8 is more than 10,000 times larger than H_CO2.

In order to quantitative numbers, we must determine the ion concentrations. We can do this by assuming that the solution started out neutral and that the total positive ions exactly balance the total negative ions:

[H⁺] = [OH^-] + [HCO₃^-] + 2[CO₃^2-]

Using the equilibrium relations derived before, we can rewrite this expression in terms of equilibrium coefficients, the Henry’s Law Constant, and the partial pressure of CO₂:

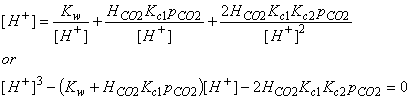
For a temperature of 298 K and a CO₂ mixing ratio of 350 ppmv, the pH of a solution of water and dissolved CO₂ will be 5.6. Because atmospheric CO₂ is always there, a pH of 5.6 is considered the pH of pure rainwater.

5.1.3. Sulfur dioxide / water equilibrium

After SO₂ is absorbed into cloud drops (H(298 K) = 1.2 M atm^-1), it ionizes (step 3) to form bisulfite (HSO₃^-) and sulfite (SO₃^2-) ions by the reactions:

(1) SO₂(g) + H₂O <==> SO₂^.H₂O

(2) SO₂^.H₂O <==> H⁺ + HSO₃^- ; HSO₃^- is the bisulfite ion

(3) HSO₃^- <==> H⁺ + SO₃^2- ; SO₃^2- is the sulfite ion

(4) H₂O <==> H⁺ + OH^-

These reactions have the equilibrium constants:

H_SO2= [SO₂^.H₂O ]/p_SO2

K_s1 = [H⁺][HSO₃^-]/[SO₂^.H₂O]

K_s2 = [H⁺][SO₃^2- ]/[HSO₃^-]

K_w = [H⁺][OH^-] ; This is called the ion product of water: K_w = 10^-14 M² @ 298 K.

The concentrations of the dissolved species are:

[SO₂^.H₂O] = H_SO2 p_SO2

[HSO₃^-] = K_s1[SO₂^.H₂O]/[H⁺] = H_SO2 K_s1 p_SO2/[H⁺]

[SO₃^2- ] = K_s2[HSO₃^-]/[H⁺] = H_SO2K_s1K_s2 p_SO² / [H⁺]²

Let total sulfur that is in the IV oxidation state in the aqueous solution be written as:

[S(IV)] = [SO₂^.H₂O] + [HSO₃^-] + [SO₃^2- ]

Writing all of the concentrations as a combination of constants and [H⁺]:

[S(IV)] = H_SO2 p_SO2 {1 + K_s1/[H⁺] + K_s1 K_s2 /[H⁺]²}

Therefore, we can write total dissolved sulfur as:

[S(IV)] = H_S(IV)* p_SO2

The effective Henry's Law coefficient is:

H_S(IV)* = H_SO2 {1 + K_s1/[H⁺] + K_s1 K_s2 /[H⁺]²}

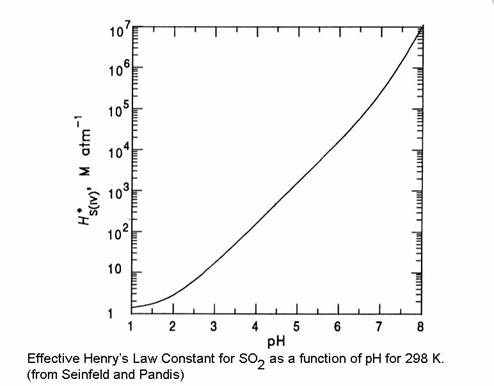
Note that H*_S(IV) is always greater than H_S(IV). Note also that the total dissolved sulfur is dependent on the pH.

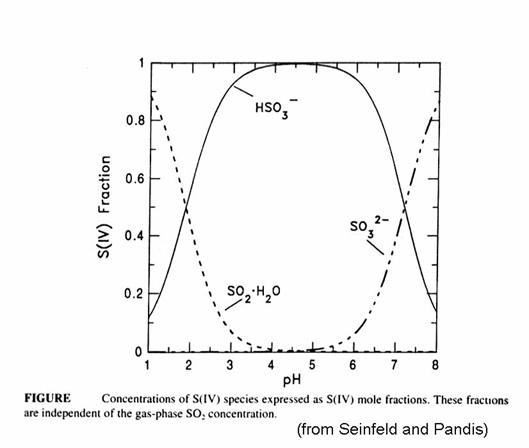
The fraction of S(IV) that is SO₂∙H₂O, HSO₃^-, and SO₃^2- is given in the next figure. Note that the bisulfite ion is the most important for much of the range of cloud water. Recall that atmospheric CO₂ creates cloud water with a pH of 5.6. The form of the sulfur becomes quite important when we think about reactions of sulfur compounds in the aqueous phase.

To find the pH of the solution, we can assume once again assume electroneutrality. Thus,

[H⁺] = [OH^-] + [HSO₃^-] + 2 [ SO₃^2- ]

[H⁺] = K_w/[H⁺] + H_SO2 K_s1 p_SO2/[H⁺] + 2 H_SO2 K_s1 K_s2 p_SO2 / [H⁺]²

or

[H⁺]³ – (K_w + H_SO2 K_s1 p_SO2) [H⁺] - 2 H_SO2 K_s1 K_s2 p_O2 = 0

By looking at the values for each of the terms, we can simplify this expression.

5.1.4. Ammonia /water equilibrium.

Ammonia is the major basic atmospheric constituent that enters aqueous solutions. It equilibrium equations are:

NH₃ + H₂O Û NH₃ ·H₂O

NH₃ ·H₂O Û NH₄⁺ + OH^-

where NH₄⁺ is the ammonium ion. The equilibrium constants has the following equations and values:

With these two equilibrium equations, we can find the ammonium ion concentration:

Thus, the total dissolved ammonia [NH₃^T] is given by:

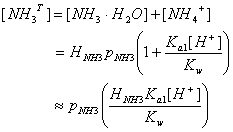
We were able to make the last approximation because for K_a1[H⁺]/K_w ~ 1.5x10^-5 10^-7 / 10^-14 >> 1. Thus, for pH less than 8, [NH₃^T] ~ [NH₄⁺]. For pH < 5, essentially all ammonia will be dissolved in the cloud water.

5.1.5. Nitric acid / water equilibrium.

After sulfuric acid, nitric acid is the most important acid that comes from pollution. It is through nitric acid that the oxidation processes that create ozone are linked to the processes that cause acid rain and aerosol formation. The equilibrium equations are:

HNO₃ + H₂O Û HNO₃×H₂O

HNO₃×H₂O Û NO₃^- + H⁺

The equilibrium constants and their values are:

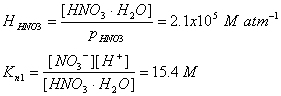
With these two equilibrium constants, we can find the nitrate concentration:

so that the total dissolved nitric acid is:

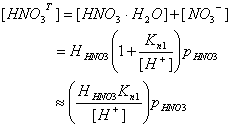
K_n1 = 15.4 M at 298 K. Thus, K_n1 / [H⁺] >> 1. Thus [NO₃^-] >> [HNO₃×H₂O]

The effective Henry’s Law constant is:

For a pH of 5, so that [H⁺] = 10^-5 M, the effective Henry’s Law Constant is ~3x10¹³ M atm^-1. Almost all of the nitric acid will be in the aqueous phase.

5.1.6. Hydrogen Peroxide / water equilibrium.

The equilibrium equations for hydrogen peroxide are:

H₂O₂(g) +H₂O Û H₂O₂×H₂O

H₂O₂×H₂O Û HO₂^- + H⁺

The partitioning between H₂O₂×H₂O and HO₂^- is given by:

We see that almost all dissolved H₂O₂ is in the form of H₂O₂×H₂O for pH values that are typical for the atmosphere (i.e., less than 5.6).

5.1.7. Ozone.

Ozone is not very soluble in water. It exists essentially entirely in the aqueous form of O₃∙H₂O.

5.1.8. List of constants.

The following table contains the Henry’s Law Constants and the Equilibrium Constants for the atmospheric constituents and equilibria discussed above. These equilibria are temperature dependent, but we will assume that the temperature is always near 298 K. for our discussions.

Selected Henry’s Law Constants and Equilibrium Constants at 298 K.
Equilibrium	H (mole L^-1 atm^-1)	K (M)
H2O ↔ H^+ + OH^-		1.0 x 10^-14
CO2 + H2O ↔ CO2∙H2O	3.4 x 10^-2
CO2∙H2O ↔ H^+ + HCO3^-		4.3 x 10^-7
HCO3^- ↔ H^+ + CO3^2-		4.7 x 10^-11
SO2 + H2O ↔ SO2∙H2O	1.23
SO2∙H2O ↔ H^+ + HSO3^-		1.32 x 10^-2
HSO3^- ↔ H^+ + SO3^2-		6.42 x 10^-8
NH3 + H2O ↔ NH3∙H2O	62
NH3∙H2O ↔ NH4^+ + OH^-		1.8 x 10^-5
HNO3 + H2O ↔ HNO3∙H2O	2.1 x 10^5
HNO3∙H2O ↔ H^+ + NO3^-		15.4
H2O2 + H2O ↔ H2O2∙H2O	7.45 x 10^4
H2O2∙H2O ↔ H^+ + HO2^-		2.5 x 10^-12
O3 + H2O ↔ O3∙H2O	0.011

5.2. Aqueous sulfur chemistry

The equilibrium processes descried above are reversible. If the partial pressure of SO₂ decreases for some reason, like dilution or surface deposition, the sulfur in the aqueous phase will remain in equilibrium with the partial pressure and will thus decrease. The situation is quite different for more oxidized forms of sulfur, sulfates, the S(VI) compounds. These have a very low vapor pressure and remain for the most part in the liquid phase. Thus, the reactions that take S(IV) to S(VI) are essential for the production of acid rain.

S(IV) can be oxidized to S(VI) by a number of chemical species, including O₃, H₂O₂, dissolved oxygen catalyzed by metals, and dissolved NO₂.

Application to the atmosphere, which has clouds and fogs.

How do we apply liquid-phase chemistry to the atmosphere? How do we compare the rates of processes that occur in the liquid phase to those that occur in the gas-phase? Recall that the reaction rate is proportional to the concentration of the reactants. In the gas phase, we usually use the units molecules cm^-3, while in the aqueous phase, we use the units M = moles/liter. Converting between these two can be a headache. However, for reactions or equilibria, it is the concentrations that matter. We can compare the gas-phase and aqueous phase rates by considering the rate in a volume of air. To calculate the rate for the aqueous phase, we need to know the volume of liquid that is in that volume of air. This value is usually called the liquid water content (LWC). In cloud physics, this is usually given units of g m^-3. There is another value that is also used: the cloud water mixing ratio, which is w_L = (volume of liquid)/(volume of air). The two are related. Since for water 1 m³ = 10⁶ g, the conversion between the two is:

LWC = 10⁶ w_L

What are typical values for w_L for different conditions? They are the following:

wet aerosol: 10^-12 - 10^-9

fog : 10^-9 - 10^-7

cloud : 5x10^-8 - 3x10^-6 , or 0.05 – 3 g m³.

Assume that a solute A is neither created nor destroyed. The distribution factor, f_A, is the ratio of the aqueous phase concentration and the gas-phase concentration, in the same units (g/(Lof air)), or other units will do.

f_A = (mass in liquid / volume of air)/(mass in air / volume of air) = concentration in the liquid in the volume of air / concentration in the gas phase.

We will denote the concentration in the liquid in the volume of air with C_A(aq) and the concentration in the gas-phase with C_A(g). Note that [A(aq)] is the concentration of A in the liquid in terms of moles/L(liquid).

So, C_A(aq) = [A(aq)] w_L, which has the units (moles/L(aq)) x (L(aq)/L(air)

C_A(g) is different from [A(g)] because it must have units of moles/L(air) if f_A is to be unitless.

Now, we can transform these relations using the Ideal Gas Law, to get the gas-phase amount in terms of the partial pressure, p_A.

p_A = C_A(g) RT implies the C_A(g) = p_A / RT.

We should make sure that we use R = 0.08205 atm L mol^-1 K^-1 and p_A in units of atm.

Further, we can transform the liquid phase concentration by using Henry’s Law:

C_A(aq) = [A(aq)] w_L = H_A p_A w_L

We will need to use the appropriate Henry’s Law Constant, which in many cases will be the effective Henry’s Law Constant.

Putting all of this together gives us the ratio of A that is in the liquid phase to A in the gas phase:

What we are really interested in is the fraction of A that is in the liquid phase, denoted as X^A_aq:

For LWC = 10^-9 l m^-3, (R T LWC)^-1 = 4x10⁴ M atm^-1. Thus, chemical species that have a Henry's Law constant, or effective Henry's Law constant much less than 4x10⁴ M atm^-1 will be mostly in the gas-phase, as in the figure. As a result, in the absence of oxidation, most SO₂ will be in the gas-phase and most HNO₃ will be in the liquid.

So, now we can put the aqueous phase reactions in the context of the atmosphere.

For a dissolved species A,

S(IV) + A(aq) ® products

In the liquid phase, the rate equation for this reaction is simply:

The units for this reaction rate are M s^-1 = moles L^-1 s^-1. To get this reaction rate in terms of liters of air, we must multiply by w_L. This will give us the reaction rate for A and S(IV) due to liquid phase the liquid phase reaction.

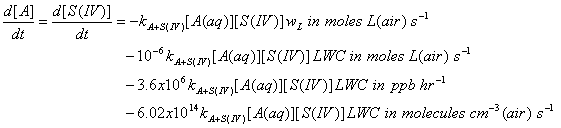
The reaction rate coefficient should have units of L mole^-1 s^-1; the concentrations are M = moles L(aq)^-1; LWC is g m^-3; and w_L is (moles L(aq)^-1)/(moles L(g)^-1).

If we want to express these equations in terms of per cent change per hour, we simply divide the third expression by the mixing ratio of SO₂ and multiply by 100:

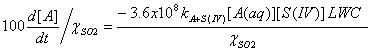
The lifetime is simply this 100 divided by this last equation, in units of hours.

We can also get the fraction converted per unit time. The fraction of sulfur converted per unit time is the conversion rate divided by the total amount of sulfur not yet converted, in both the gas and the liquid phase. The fractional rate is thus:

fraction converted per unit time = {d([S(IV)])/dt} / {p_SO2/RT + H*_SO2 p_SO2 w_L}

Now let’s look specifically at the oxidation of S(IV) to S(VI). We can see the reaction rates for typical amounts of different oxidants. The liquid-phase oxidants, H₂O₂ and O₃, are largely created in the gas-phase and absorbed into the liquid. Note that O₃ and H₂O₂ are both formed by processes involving HO_x radicals. We should expect that the greatest oxidation will occur during the day, when oxidant concentrations are largest, and will be greater in the summer than the winter for the same reason.

Because the oxidation by HOOH is by far the largest for anything but very acidic or basic solutions, we will focus on it.

The reaction pathway is given by the equations:

HSO₃^-+H₂O₂ <==> SO₂OOH^- + H₂O

SO₂OOH^- + H⁺<==> H₂SO₄

The specific rate equation is from Hofmann and Calvert (1985):

d([S(IV)])/dt = - {k_HOOH+S(IV)[H⁺][H₂O₂(aq)][HSO₃^-] }/{1 + K_HOOH[H⁺]}

where k_HOOH+S(IV) = 7.5x10⁷ M s^-1, and K_HOOH = 13 M^-1. Note that we must determine [H⁺], [H₂O₂(aq)] = H_H2O2 p_H2O2. Note that we cannot use [S(IV)](aq), but must instead use [HSO₃^-], which can be calculated from the equilibrium conditions.

This reaction rate is essentially independent of pH when we multiply all the terms together. The reason for this weak dependence is that k_HOOH+S(IV) is essentially independent of [H⁺], {H₂O₂(aq)] is independent of [H⁺], [HSO₃^-] depends on 1/[H⁺], and K_HOOH[H⁺] << 1.

For p_H2O2 = 1 ppb,

d[S(IV)]/dt = 300 mM h^-1 (ppbSO₂)^-1 (700% SO₂(g) h^-1 (g water / m³ air)^-1

The reactions on page 367 show that the immediate product is H₂SO₄, sulfuric acid.

What happens to it? It is ionized:

H₂SO₄(aq) Û HSO₄^- + H⁺ K_svi1 = 1000;

HSO₄^- Û SO₄ ^2- + H⁺ K_svi2 = 1.02x10^-2

H₂SO₄(g) Û H₂SO₄(aq) remains in liquid-phase.

Therefore, we can determine the dominant forms of S(VI):

Open and closed systems.

1. Open system.

1. Gas partial pressures are maintained at fixed values by resupply from new air or from photochemistry.

2. Not a very realistic condition.

2. Closed system.

1. gas-phase partial pressures decrease with time.
2. More representative of actual behavior.
3. Masses of elements, such as S, N, C are conserved in the process.

Let us consider what happens in a closed system.

In an open system, [H₂O₂(aq)] = H_H2O2 p⁰_H2O2. In this case, the aqueous phase H₂O₂ is independent of LWC.

In a closed system, initial H₂O₂ is split between the gas and aqueous phases, as the cloud forms:

[H₂O₂]_total = (p_H2O2/RT) + [H₂O₂(aq)]_closed w_L

where recall that w_L has units of L liquid / L air and R = 0.082 (atm L)/(mole K).

If we are in equilibrium, then Henry’s Law holds and:

[H₂O₂(aq)]_closed = H_H2O2 p_H2O2

If initially there was no cloud, then the conservation equation for H₂O₂ becomes:

p^o_H2O2 = p_H2O2 + [H₂O₂(aq)]_closed w_L RT

= [H₂O₂(aq)] {(1/H_H2O2) +w_L RT}

Combining these equations, we get:

[H₂O₂(aq)]_closed = (H_H2O2 p^o_H2O2) / (1 + H_H2O2 w_L RT)

Note that [H₂O₂(aq)] decreases as LWC or w_L increases. More water means that more H₂O₂ can be accommodated in the aqueous phase. The open system is represented by the dashed lines. For the closed system, because p_H2O2 is proportional to [H₂O₂(aq)], p_H2O2 drops as [H₂O₂(aq)] drops. In addition, because p_H2O2 is proportional to [H₂O₂(aq)], the fraction of H₂O₂ that is in the aqeuous form [H₂O₂(aq)] increases as the LWC increases.

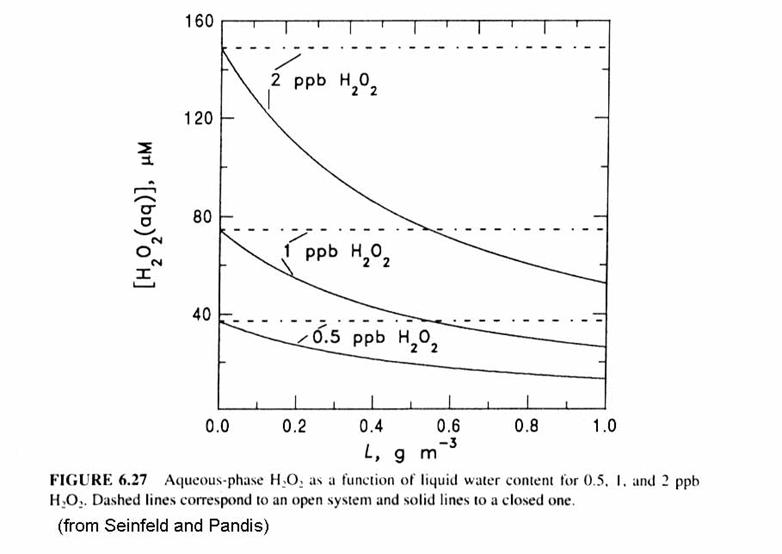
More sulfate is produced in the open system than the closed system, as in the figure below. This makes sense: the oxidants and SO₂ are being constantly replaced and is thus able to continue the conversion of S(IV) to S(VI).

Low solubility gases, like ozone, maintain aqueous phase concentrations that are similar to that for open systems. For example, if w_L = 10^-6, T = 300 K, then H_O3 w_L RT = 0.0113 10^-6 0.082 300 = 2.8 x 10^-7, which is much smaller than 1 and can be ignored.

[O₃(aq)]_closed = (H_O3 p^o_O3) / (1 + H_O3 w_L RT) ~ (H_O3 p^o_O3)

We can do the same thing for dissociating species, such as HNO₃:

[HNO₃(aq)] +[NO₃^-] = (H^*_HNO3 p_HNO3) / (1 + H^*_HNO3 w_L RT)

where

H^*_HNO3 = H_HNO3 {1 + K_n1 / [H⁺]}

Consider a cloud forming in clear air that contains SO₂ and H₂O₂.

1. Equilibrium is readily established.
2. Concentrations of ions will adjust as the reactions proceed so that electroneutrality is maintained.
3. The concentrations of all species can be defined by their equilibrium constants and partial pressures, except for sulfate and bisulfate, which are strictly in the aqueous phase.
4. The reactions will proceed until either H₂O₂ or SO₂ are depleted. If H₂O₂ is depleted first, then the SO₂ will move further downwind and get oxidized to S(VI) by either gas-phase or aqueous phase processes downwind.

Global transport models suggest that gas-phase oxidation and liquid phase oxidation are about equally important for global SO₂ emissions, even though the rates of oxidation in cloud water are several 10’s of percent per hour, while gas-phase oxidation is at most a few percent per hour. While clouds cover roughly half of Earth’s surface at any given time, they occupy a much smaller volume of the troposphere at any given time.

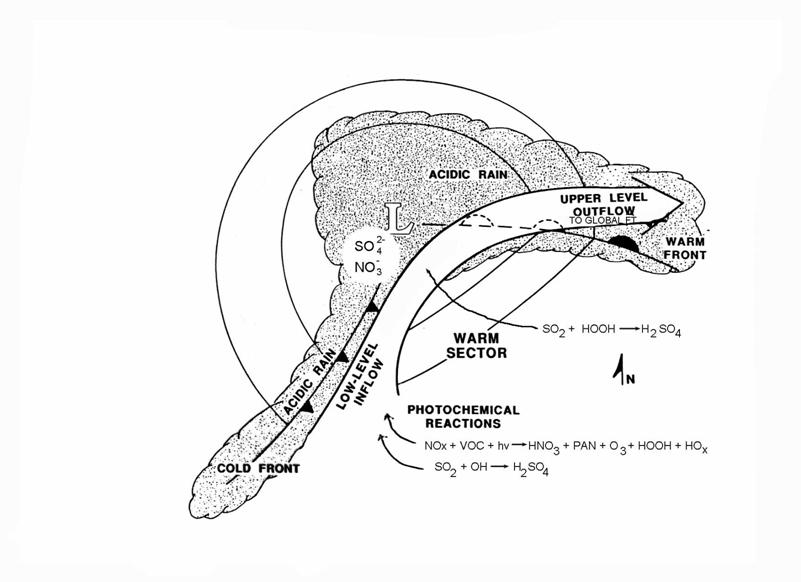
Once the sulfate aerosol is in cloud drops, it can come down as precipitation. The figure below depicts the processes that occur in a rain storm. The photochemical constituents are drawn up into the storm in the low level inflow. Aqueous phase conversion of SO₂ to sulfate occurs. Rain out deposits some of this sulfate on Earth’s surface. What is not rained out can be delivered to the global free troposphere by the upper level outflow. This sulfate can then travel great distances as aerosol before it is brought down to lower levels by subsidence of it air parcel, where it can be deposited by dry or wet processes.

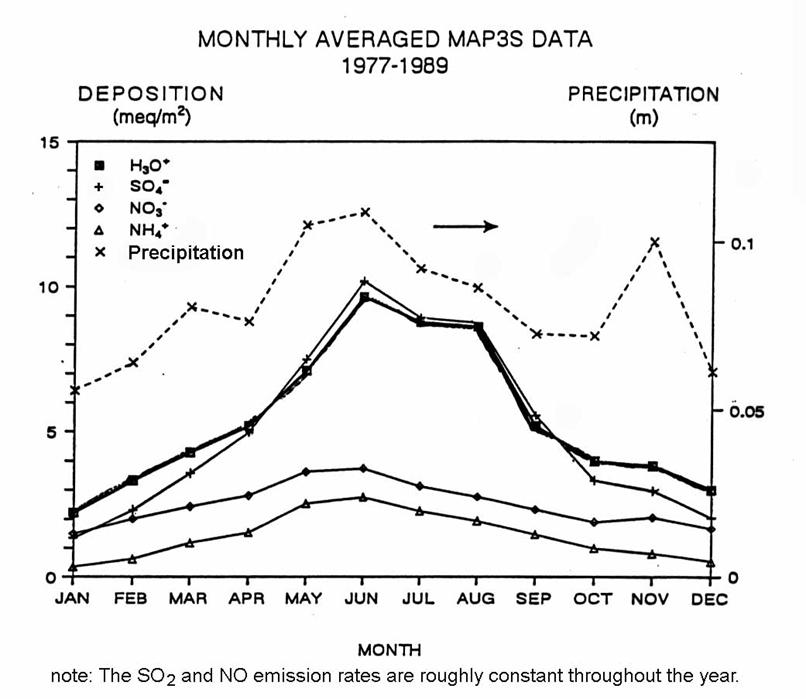
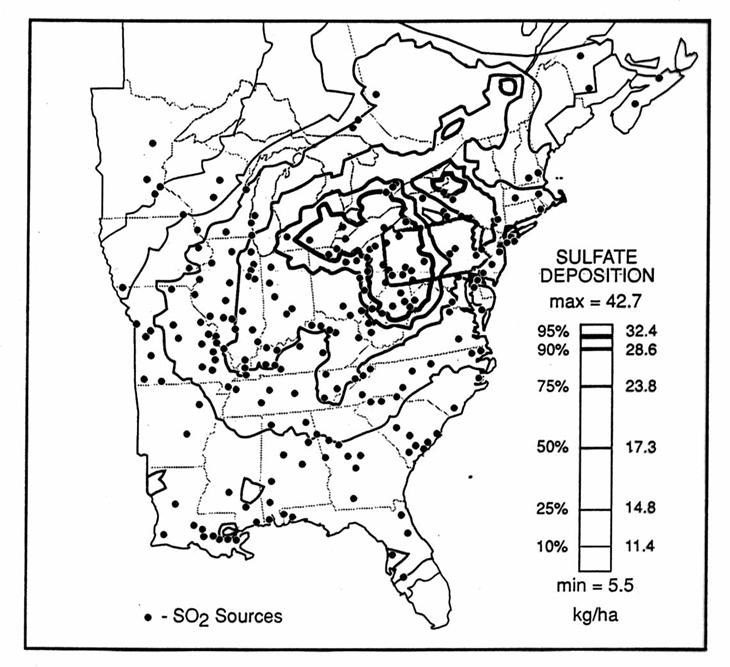
The pattern of sulfate deposition for the Eastern United States is shown in the following figure.

The figure below shows the annual variation of deposition for sites in the Eastern United States. There is a clear peak in deposition during the summer months. This peak is not due to increases in SO₂ and NO emissions, which are roughly constant over the whole year. What could be the cause of this summertime increase?