Meteo 532 Atmospheric Chemistry

Problem set #4 – Solutions

Fall 2003

4.1 Tropospheric ozone production and loss.

a) Write down the expression for the net tropospheric ozone production:

d[O₃]/dt = P-L=? Remember to include the terms that destroy ozone as well as the ones that make ozone. Assume that RO₂ is negligible.

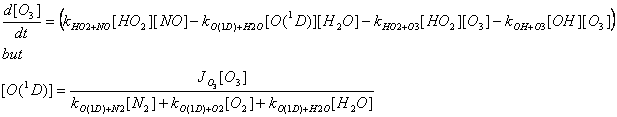
b) We know that ozone is actually produced from NO₂+hv®NO+O, followed by O+O₂+M®O₃+M. Why does the expression for d[O₃]/dt contain no terms for these two reactions?

Ozone production is from the two reactions listed above. However, they also participate in a reaction sequence that creates no new ozone – the NO_x photostationary state. In this case, these two reactions balance the destruction of ozone by NO+O₃ ® NO₂+O₃. Thus, all the production and destruction of ozone that is not balanced in the NO_x photostationary state must pass through the reactions in the rate equation in a). We could list the rate equation with the two reactions listed above, but then we would need to realize that a lot of the cycling was simply the null cycle of the NO_x photostationary state.

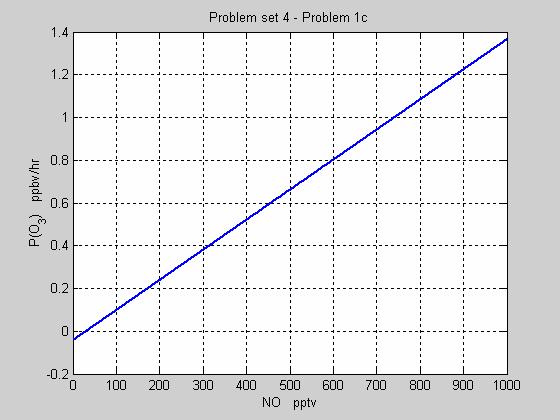
c) Plot the net ozone production rate, in ppb hr^-1, at 10 km altitude as a function of NO from 1 to 1000 pptv for HO₂=5 pptv, OH=0.5 pptv, O₃=60 ppbv, H₂O=200 ppmv, and J_O3=2x10^-5 s^-1? Assume also the p=250 mb and T=235 K and that [RO₂] is negligible.

% m532_ps4_p1.m calculates ozone net production and plots it

% as a function of NO

%

% Find the number density at 10 km.

T = 235;

p = 250;

M = 2.69e19*(273/T)*(p/1013);

%

% Establish the rate coefficients

%

JO3 = 2e-5;

k_ho2_no = 3.5e-12*exp(250/T);

k_o1d_h2o = 2.2e-10;

k_o1d_n2 = 1.8e-11*exp(110/T);

k_o1d_o2 = 3.2e-11*exp(70/T);

k_ho2_o3 = 1.0e-14*exp(-490/T);

k_oh_o3 = 1.7e-12*exp(-940/T);

%

% Set up a vector for NO between 1 and 1000 pptv

for i=1:1000

NO(i)=i;

end

%

% Find the concentrations of the trace chemicals

HO2_c = 5e-12*M;

OH_c = 0.5e-12*M;

O3_c = 60e-9*M;

H2O_c = 200e-6*M;

NO_c = NO*1e-12*M;

N2_c = 0.79*M;

O2_c = 0.20*M;

%

% Solve the rate equation

%

f = (k_o1d_h2o*H2O_c)/(k_o1d_h2o*H2O_c+k_o1d_n2*N2_c+k_o1d_o2*O2_c);

PO3 = (k_ho2_no*HO2_c*NO_c)-(JO3*O3_c*f+k_ho2_o3*HO2_c*O3_c+...

k_oh_o3*OH_c*O3_c);

PO3_ppbhr = (1e9/M)*PO3*3600;

%

% Plot PO3 as a function of NO

plot(NO, PO3_ppbhr,'linewidth',2)

grid

xlabel('NO pptv')

ylabel('P(O_3) ppbv/hr')

title('Problem set 4 - Problem 1c')

d) Consider the set of reactions:

OH+CO®H+CO₂

H+O₂+M®HO₂+M

OH+O₃®HO₂+O₂

HO₂+NO®OH+NO₂

HO₂+O₃®OH+2O₂

Write down the rate equation for OH, assuming that the second reaction is much faster than the others.

e) Assuming that OH and HO₂ are in steady-state, write down the [HO₂]/[OH] ratio in terms of [NO], [CO], [O₃], and the rate coefficients.

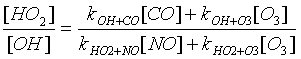
4.2 Variation of ozone production with [NO].

HO_x, the sum ofOH+HO₂, has the rate equation:

d[HO_x]/dt=P(HO_x)–{2k_HO2+HO2[HO₂][HO₂]+2k_OH+HO2[OH][HO₂] +k_OH+NO2+M[M][NO₂][OH]}

where P(HO_x) is the production rate (molecules cm^-3s^-1) of HO_x, OH or HO₂and the three expressions in brackets are three loss mechanisms for HO_x. HO₂+HO₂®HOOH+O₂ dominates when NO is low, OH+HO₂®H₂O+O₂ dominates when NO is about 100 pptv, and OH+NO₂+M®HNO₃+M dominates when NO is greater than a few hundred ppt. In each one of these NO regimes, we can assume that only the dominant HO_x loss reaction is occurring.

Assume that [HO_x] approximately equals [HO₂], that OH, HO₂, and thus HO_x are in steady-state, that the relationship that you derived for[HO₂]/[OH] in problem 4.1, section e applies, and that P(HO_x) is 10⁷molecules cm^-3s^-1, COis 100 ppbv, O₃ is 40 ppbv initially, p = 1000 hPa, T=298 K, and RO₂ is negligible.

Using the equations in problem 4.1, section d, determine the analytical expressions for [OH],[HO₂], and P(O₃) in terms of P(HO_x), [NO], [CO],[O₃], and rate coefficients for the three NO regimes. For this problem, P(O₃) =k_NO+HO2[NO] [HO₂].

Low-NO_x regime – the main loss is HO₂ + HO₂ ® HOOH + O₂.

Thus,

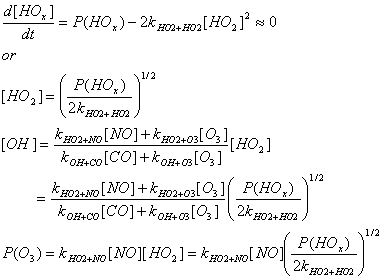
Mid-NO_x regime – the main loss is OH + HO₂ ® H₂O + O2.

Thus,

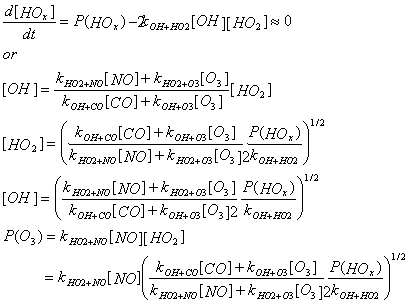
High NO_x Regime – The main loss is by OH + NO₂ + M ® HNO₃ + M

We see that in the low and mid NO_x regimes, [OH], [HO₂], and P(O₃) all depend on the square root of P(HO_x), while in the high-NO_x regime, they all depend linearly on P(HO_x).

For most cases, the reaction of HO₂ with NO is much greater than its reaction with O_3, even in much of the low-NO_x regime. If we assume this is the casem then in the low NO_x regime, both [OH] and P(O₃) depend roughly linearly with NO, while [HO₂] is independent of NO. In the mid-NO_x regime, [HO₂] depends roughly on the inverse square root of NO, while [OH] and P(O₃) depend on the square root of NO. In the high-NO_x regime, [HO₂] depends roughly on the inverse square of NO (because NO and NO₂ are related through the NO_x photostationary state), while [OH] and P(O₃) depend rouhgly on the inverse of NO. Thus, as NO increases, HO₂ is at first indepent, but then drops off at an increasing greater power of NO as NO increases. On the other hand, OH and P(O₃) show the same behavior: they initially increase roughly linearly with NO, level off at some value, and then begin to dcrease linearly with NO.

4.3. Ozone production from the imbalance in the NO_x photostationary state.

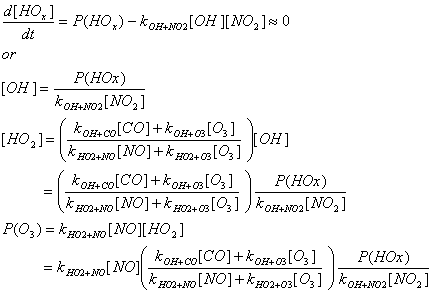
Consider the [NO₂]/[NO] relationship given above – the actual photochemical state (APS), and compare it to the NO_x photostationary state relationship (PSS). Prior to the ability to measure the oxidants HO₂ and CH₃O₂, researchers tried to determine the sum of [HO₂]+[CH₃O₂] by looking at the deviation of the APS from the PSS, where [NO], [NO₂], J_NO2, and [O₃] were all measured. They assumed that k_HO2+NO and k_CH3O2+NO were the same.

a) Derive the equation for [HO₂]+[CH₃O₂] in terms of the equation just above

b) For T=298 K, p=1013 hPa, J_NO2 = 8 x 10^-3 s^-1, O₃=60 ppbv, and NO_x = 1ppbv, what is the ratio [NO₂]/[NO] according to the PPS relationship?

For these conditions, [M]=2.46x10¹⁹ cm^-3, [O₃] = 60x10^-9 2.46x10¹⁹ = 1.48x10¹² cm^-3;

[NO_x] = [NO] + [NO₂] = 10^-9 2.46x10¹⁹ = 2.46x10¹⁰ cm^-3.

c) If we include 10 pptv of both HO₂ and RO₂, what is the deviation of the APS from the PSS, in the form:

dev = ([NO₂]/[NO]_APS - [NO₂]/[NO]_PSS)?

For APS, k_HO2+NO = 8.1x10^-12 cm³ molecule^-1 s^-1. [HO₂] = 2.46x10⁸ cm^-3.

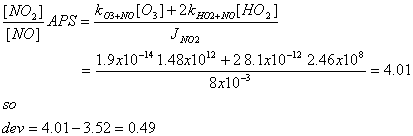
d) Measurements have uncertainties: for NO, 7%; for NO₂, 10%; for O₃, 3%; for k_NO+O3, 10%; and for J_NO2, 5%. The measurement uncertainty can be found by taking the expression:

err = [NO₂]/[NO] – k_NO+O3 [O₃]/J_NO2,

taking the derivative of err with respect to the 5 parameters; taking the square root of the sum of the squares of the resulting terms. (Note: you can easily get each term in the derivative into the form ¶A/A. For example: ¶[NO₂]/[NO] = (¶[NO₂]/[NO₂])([NO₂]/[NO]).) How does the deviation from c) compare to the measurement uncertainty? What does this tell you about this measurement technique for [HO₂] + [RO₂]?

Putting these fractional errors in absolute terms,

[NO₂] = (3.51/(1+3.51))2.46x10¹⁰ = 1.91x10¹⁰ cm^-3

[NO] = (1/(1+3.51)) 2.46x10¹⁰ = 5.45x10⁹ cm^-3.

D[NO] = 0.07 5.45x10⁹ = 3.8x10⁸ cm^-3

D[NO₂] = 0.10 1.91x10¹⁰ = 1.91x10⁹ cm^-3

D[O₃] = 0.03 1.48x10¹² cm^-3 = 4.44x10¹⁰ cm^-3

Dk_NO+O3 = 0.10 1.9x10^-14 = 1.9x10^-14 cm³ molecule^-1 s^-1

DJ_NO2 = 0.05 8x10^-3 = 4x10^-4 s^-1

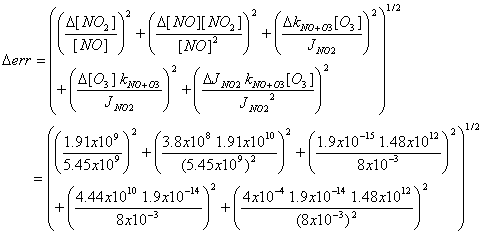
Derr = 0.59

Thus Derr is very similar to the deviation that we expect from the NO_x photostationary state. This suggests that using the deviation from the NO_x photostationary steady state to determine the instantaneous ozone production, or the concentrations of HO₂ and RO₂, is very difficult and not statistically significant.

4.4 Chlorine oxidation of hydrocarbons

As pollutants from the urban centers on the East Coast are swept out over the Atlantic Ocean, they are mixed with the marine air which is rich with chlorine and other halogens. If the chlorine in sea salt is converted by some reaction mechanism into gaseous atomic chlorine, the resulting Cl will react with hydrocarbons, starting the oxidation process, just as OH does. Thus, oxidation of hydrocarbons by Cl could lead to O₃ production, just as oxidation by OH does.

Some reactions on surfaces have been observed to convert the chlorine in NaCl into gaseous Cl₂. The main chemical loss for Cl₂ is photolysis into 2 chlorine atoms. The chlorine atoms, Cl, can then react with hydrocarbons. For this problem, we chose ethane, C₂H₆, as the hydrocarbon. The beginning of this reaction sequence can be described by the reactions:

Cl₂ + hn ® 2 Cl J_a (ra)

C₂H₆ + Cl ® C₂H₅ + HCl k_b (rb)

C₂H₆ + OH ® C₂H₅ + H₂O k_c (rc)

The temperature is 298 K. The pressure is 1013 hPa. For these conditions, k_b = 5.7 x 10^-11 cm³ molecule^-1 s^-1 and k_c = 2.4 x 10^-13 cm³ molecule^-1 s^-1. Assume that the C₂H₆ mixing ratio is 10 ppbv, and that [OH] = 3 x 10⁶ molecules cm^-3. The photolysis frequency for Cl₂ is 1.6 x 10^-3 s^-1.

[M] = 2.46x10¹⁹ cm^-3 implies that [C₂H₆] = 2.46x10¹¹ cm^-3.

a) If the mixing ratio of C₂H₆ is 10 ppbv, what are the lifetimes of OH and Cl?

t_OH = (k_c [C₂H₆])^-1 = 17 s

t_Cl = (k_b [C₂H₆])^-1 = 0.071 s

b) We want to know if Cl is an important oxidant in the marine environment. What Cl concentration is required for Cl to oxidize ethane as fast as OH does?

To determine the Cl concentration that will have the same C₂H₆ destruction rate as OH, we multiply [OH] by the ratio of the OH reaction rate coefficient to the Cl reaction rate coefficient.

This value of [Cl]_equivalent = (2.3x10^-13/5.7x10^-11) 3x10⁶ = 1.2 x 10⁴ cm^-3

c) What is the expression for the steady-state concentration of Cl?

Assume that we have 10 pptv of Cl₂

d) The observed mixing ratio of Cl₂ in one experiment is about 50 pptv near midday. With this source of Cl, what fraction of the oxidation of ethane is by Cl and what fraction is by OH? Is Cl an important oxidant?

OH: 2.3x10^-13 3 x 10⁶ = 6.9 x 10^‑7 s^-1

Cl: 5.7x10^-11 2.8x10⁵ = 1.60 x 10^{-5 s-1}

total: 1.665 x 10^-5 s^-1.

96% is by Cl and 4% is by OH. Cl can be an important oxidant in the marine boundary layer.

e) What is the lifetime of C₂H₆ in the marine environment, assuming that the diurnal average of [OH] and [Cl] are 1/3 of their midday values? Assume that the chlorine concentration is maintained at the value obtained in part (d), even though C₂H₆ is being oxidized.

t_C2H6 = (1.665x10^-5/3)^-1 = 1.80x10⁵ s = 2.1 days