
The Human Population System
Contents:
- Introduction
Introduction
Most people would consider the study of human population dynamics to be outside the realm of the earth sciences, so why is it included in this book? The reason is simply that the growing human population is the root cause of all the environmental problems -- if we care about the future well-being of our planet and our environment, we cannot ignore the dynamics of the human population. To worry about environmental problems while ignoring the population problem is like treating the symptoms of a disease without ever trying to find a cure. This disease that is population growth has the potential to make our future a very unpleasant one, but there are definite possibilities for halting population growth and making our future stable and comfortable; we will explore these possibilities in by means of several STELLA models described below.
The goals of this chapter are: 1) to explore and better understand the dynamics of human population growth through a series of models; and 2) to gain a better appreciation of the problem by looking at the history of growth, the implications of continued growth, and the limitations to growth.
History of Population Growth
Here we examine what is known about the history of the human population in order to gain a better understanding of the context of the current concern with population growth and also to see how population has behaved in the past. How does recent population growth compare with what has occurred in the past? Are there any episodes from the past that may give us some sense of how the system might behave in the future?
Not surprisingly, little is known about the global population back beyond a few hundred years, but demographers have extrapolated and interpolated to provide an approximate history (understand that it gets more approximate the further back in time you go) that is shown in the figure below.

Note that in the graph on the left, we go all the way back to 10,000 BC. Plotted at this scale, the history is completely dominated by the extraordinary population increase in the last portion of our history. Even if we look at a more restricted part of this history, beginning at 500 BC, the history is still dominated by the growth of the last 100 years. Note that these graphs also include a projection into the future, to the end of the next century, using the predictions of the United Nations. The population is predicted to peak at around 12 billion, but we should remember that this is just a prediction and it is a very difficult predication to make. For instance, twenty years ago, it was thought that the population would level off at about 8 billion. So, the value at which the current growth levels off is not a very well-constrained estimate.
Looking at the above graphs, the earlier history of population growth seems entirely unremarkable, but this is partly a problem of the scale on the vertical axis. As can be seen in the graph below, if you plot the vertical axis at a log scale, we expand the lower parts of the graph, allowing us to see that indeed, there are some interesting variations in the growth rate. If the history of population were described as a strict exponential function, with a constant percent of annual growth, this graph should be a straight line. The fact that it is not means that the percent of growth has been increasing over time, especially during the last hundred years.
Some demographers have broken this history up into three different growth spurts, the two earlier ones being separated by periods of no growth, as indicated on the graph. The first growth spurt is sometimes called the primary growth cycle, and it shows up well if we look at the period of time from 5,00 BC to 200 AD, a period of time that includes the rise and fall of the Greek and Roman worlds, as well as a big increase and small collapse in China. This first growth cycle, shown below, is dominated by these three regions; other parts of the world, as far as we know, did not participate in this growth.
This growth spurt came to an end in both places at roughly the same time and is related to the fall of the Roman empire and the fall of the Han empire in China. The Han empire encountered problems in the form of invading nomadic peoples, such as the Huns, from the region that is now Mongolia (this is when the Great Wall as built); these invasions led to political disorder and infrastructure problems that halted population growth. The Chinese eventually resisted these invasions, forcing them off to the west, towards Europe, where they pressured an already over-extended Roman empire, accelerating its demise. The end of this classical period signaled the beginning of the Dark Ages, where disorder reigned and as a result, the global population declined by a little.
The next growth period began in the Medieval Ages, with the rise of the Sung Dynasty in China and the organization of Europeans into feudal societies.
The graph above shows that in this cycle, things really took off around the year 1000, and only lasted for a few hundred years. As with the previous cycle, as these regions became highly organized, they experienced surges in their populations. Also like the previous cycle, this one came to an end when the organization was lost. In China, once again, invaders from the region of Mongolia, led by Genghis Khan, threw the empire into disarray and killed many millions of Chinese. At about the same time, Europe fell into a sharp decline due to the very rapid spread of the bubonic plague, which led to a reduction in Europe's population of nearly 20 million.
The most recent growth spurt, shown below, has its roots in the agricultural and industrial revolutions of the 19th century. Technological improvements increased food production, economic expansion, medicine, and the result was a decrease in the death rate; birth rates do not respond as quickly as death rates, so the population grows exponentially or even faster. Where will this cycle end? Will it be at 12 billion, as predicted by the UN? What will cause the end of this cycle?
General Models of Population Dynamics
In this section ,we briefly examine the structure and behavior of a variety of models that might apply to population growth under a variety of conditions. These models are all relatively simple in the sense that all individuals in the population are represented by a single reservoir rather than representing different age segments of the population with different reservoirs. But we should keep in mind that the goal of these particular models is to learn some general things about different patterns of population growth.
1. Simple Exponential Growth
The simplest model we can imagine consists of one reservoir representing all of the individuals of a population, with two flows. One flow represents births, and it is a function of the birth percent and the number of individuals in the population. The other flow represents deaths, and it is a function of the death percent and the number of individuals in the population. We will use one year as our basic time unit, and the quantity in the reservoir represents the number of individuals. The structure of this system and the equations underlying it are shown in the figure below. Use this information as a recipe to create a version of this model in STELLA.
1. Experiments
Study this system carefully and answer the following questions on your way to developing a prediction. What kind of a feedback mechanism is represented by the Deaths flow? What kind of feedback is represented by the Births flow? What will each flow tend to do? Which flow (feedback mechanism) will dominate? After you've made a detailed prediction, proceed as follows:
i) Run the model for 100 years with a time step of 1.0. Study the results and compare them with your prediction. How would you describe the rate of change of the population in this model? Is there a constant rate of change?
ii) Change the value of the birth percent to 0.10 and death percent to 0.15; predict what will happen, run the model for 100 years, and study the results.
iii) At this point, you should be able to successfully predict what will happen if you make the birth percent the same as the death percent. If you are unsure, run the model in this condition.
iv) Now add a new converter labeled Log Population and add a connecting arrow from the Population reservoir to Log Population. Double-click on Log Population and make it equal to LOG10(Population), then exit this window. Next, double-click on the graph and plot Population and Log Population on the same graph. Reset the Birth Pct to 0.15 and the Death Pct to 0.10, then predict how Log Population will change before running the model for 100 years. After studying the result, you will be able to look at the earlier plot of the history of population growth and see that the recent explosion goes beyond simple exponential growth. What does this tell you about the percentage of growth over time?
This model, as defined in the figure above, represents exponential growth, characterized by an increasing rate of change, but a constant percentage of change; this type of growth is a fairly good model for describing what has occurred so far in the history of the human population (although as you learned in the last experiment, the population growth spurt is much more dramatic than can be achieved by simple exponential growth). In just a bit, we will explore what happens if we extend this type of growth into the future.
2. S-Shaped Growth and the Concept of Carrying Capacity
Not many populations grow exponentially for very long -- there are various limitations imposed by the world in which the population grows. In many cases, a population will reach what is called the carrying capacity of its ecosystem, and as this capacity is reached, the population dynamics change and approach a steady state (births = deaths). This kind of growth behavior is simpler than you might expect, and results from some basic assumptions. As an example, consider the following. We will make a simple modification to the model used above. Let's assume that as the population increases, the population density goes up, making it easier for diseases to spread, and also resulting in fewer resources per individual, which lowers the health of the average individual and making them more susceptible to disease. The net effect is that as the population increases, the death percent increases.
Changing the Model
To represent this in the model, draw an arrow connecting Population to the Death Pct converter, then double-click on Death Pct and make it equal to Population. Now, click the Become Graph button in the lower left of this window and you will see another window appear -- one that has a graph on the left and two columns one the right. The graph should have Population along the x-axis and Death Pct along the y-axis; each axis also has boxes that represent the lower and upper values for each axis. Adjust the values in these range boxes so that Population goes from 0 to 10,000 (leave out the comma) and Death Pct goes from 0 to 1.0. The graph has a grid inside it; the number of vertical lines in this grid is controlled by the number of data points, which is specified in a box near the lower left of the window; leave this at 11. If you position the cursor along one of the vertical lines in the grid and click, you will begin to create a graph, which can be completed by clicking along each of the vertical lines in the grid. Try this and you will see that a set of values appears in the Output column on the right side of the window; you can also control the graph by selecting an input value and then typing the desired output value in the box below the column. You can use either method to construct a graph that is identical to the one shown below. When you have finished making the graph, click on the OK button to exit the window; you'll see that the Death Pct converter now has a squiggle in it, signifying that there is a graph embedded in this converter. The program will use this graph in the following way -- at each point in time, the program will calculate what the population is, then it will use the graph you just made to see what value for the Death Pct it will use to make the next set of calculations that will take it to the next point in time. Use the information in this figure as a recipe for making the necessary changes.
2.Experiments
i) Make these modifications and then predict what will happen. Run the model for 100 years with a time step of 1.0. Study the results and explain why the system evolves as it does. Why does the population reach a stable level? What is the relationship between the birth percent and death percent at the point of stabilization?
ii) First try changing the Birth Pct, and then the Death Pct graph and study the results carefully until you have a good sense of what determines the stabilization point for this system.
3. Overshoot and Collapse
In the last model, the population found its steady state in a smooth manner; the rate of change decreased as the carrying capacity was approached. But this is not always the case; sometimes the population's growth rate does not decline fast enough as the carrying capacity is reached, leading to overshoot, which is usually followed by a collapse. One way of interpreting this is that the population does not process information about its condition fast enough to change its growth rate. For instance, if humans do not communicate the nature of the problem of population growth and do not communicate ways to solve the problem, we will likely overshoot our carrying capacity and a catastrophic population collapse is likely to follow.
Yeast growing in grape juice provide a good example of overshoot and collapse behavior. The yeast go after the sugar in the juice and in the process of metabolizing that sugar, they produce alcohol and carbon dioxide. As they consume the sugar, they also reproduce and their reproductive rate is dependent on the availability of food. Within a few days, at room temperature, the yeast population soars and the juice is bubbling from the release of so much CO2. But, the alcohol is a pollutant as far as the yeast are concerned and as their population rises, so does the level of alcohol. If there is enough sugar in the juice, the yeast will eventually produce so much alcohol that they start to die off rapidly and as the sugar reservoir is depleted, their reproductive rates plummet, leading to a total collapse of the population. So, in turning the juice into wine, the gluttonous, know-no-restraint yeast do themselves in.
This kind of a system is a bit more complex than the previous ones since we need to install another reservoir, representing the resources or some other kind of limiting quantity. Here, we will simply call this new reservoir Resources, and imagine that it represents things like energy and mineral resources, which can be thought of as finite resources (at least to begin with; we can explore the concept of recycling in a bit). The structure of this system, and the equations and graphs that define it are shown in the figure below; note that once again, it includes a graph in the Death Pct converter, but in this case, the Death Pct is a function of the amount of resources per capita.
The graph relating the death percent to the resources per capita effectively says that when resources are abundant, the death percent is not affected; it remains at a constant level reflecting things like disease and old age. But, once the resources per capita drops below a certain value (10 in this case), the death percent begins to increase, reflecting the idea that with fewer resources, living conditions will deteriorate, making survival more difficult.
3. Experiments
i) After you have constructed this model, take time to make a careful prediction about how the Population and Resources will evolve over time. This system is a bit harder to figure out, but it may help to consider the differences between the birth and death percents at various points in time. Then run the model for 100 years with a time step of 0.5 and see what happens. How accurate was your prediction? Can you explain what happened?
ii) Next, let's see what happens if we say that these resources are not finite -- that there is some process that adds to the resources. We can do this by adding an inflow to the Resources reservoir. Call this flow New Resources, and give it a constant value of 50 (this will be 50 resource units per year). How will this affect the model? Run the model for 100 years after making a careful prediction and study the results. What determines the stabilization point of the population? This is a relatively complex model, and you may have to experiment with some variations in order to understand what is going on here.
iii) Now, let's consider the effects of recycling on this system. How can we represent recycling here? One way to do it is to say that the inflow into the Resources reservoir is a function of the outflow. So, if we say that recycling returns 25% of the consumed resources (this is pretty good, really), then we need to draw a connector arrow from the Consumption flow to the New Resources flow and then redefine New Resources so that it is equal to 0.25 times the Consumption. Make this change, then predict what will happen. You can think of the experimental control here as the case where there was no inflow into the Resources reservoir.
iv) Finally, let's explore what happens when we combine the constant inflow of 50 units and the recycling contribution, so that the New Resources flow is defined as 50+(consumption*.25). As before, make a prediction before running this model and then study the results until you can thoroughly explain why the system behaved in the way it did.
v) It is worth realizing that until now, we have not altered the birth rate in this model; we assumed that it remained constant. But in reality, the birth rate will also change as living conditions change. It is generally observed that the birth rate in wealthier countries is less than that in poorer countries, and the birth rate is also lower in countries where the female literacy rate is higher. So, we might consider the possibility that as the resources per capita increase, the birth rate will decrease. We could easily incorporate this into our model by drawing a connector arrow from the resources per capita converter to the birth percent converter and then making the birth percent be a graphical function of the resources per capita. The precise form of this graph, relative to the death percent graph, is extremely important, as you might imagine. To begin with, we will employ a graph with the following characteristics -- identical to the death percent graph except that at low values of resources per capita (below 5), the birth percent begins to decrease again, until it is 0 when resources per capita are 0. For these experiments, remove the New Resources inflow into the Resources reservoir in order to simplify things a bit. How will this modified system behave? As before, make a prediction and then run the model for 100 years, graphing both reservoirs, the resources per capita converter, and the death and birth percents. As variations on this model, try making the birth percent first higher and then lower than the death percent at high resource per capita values -- this will lead to initial population increase and decrease, respectively.
If you want to experiment further, think of how you might incorporate increased efficiency of resource use. The thinking here is that as resources become more scarce, there is a greater incentive to conserve by using less and wasting less, which amounts to being more efficient.
4. Something Entirely Different -- Oscillations
In the last set of models, we had two reservoirs that were coupled to each other in the sense that the fate of each reservoir was somehow tied to the other. Specifically, we had it set up so that the outflows of each reservoir were affected by the size of the other reservoir. It turns out that if we make some small changes to the system structure, we get a very different kind of system behavior; one that is quite unexpected.
In this set of experiments, we'll make the population dependent in some way on pollution in the environment, and we will keep track of pollution as a reservoir. The pollution reservoir is added to by an inflow called New Pollution, which is defined as being a function of the pollution created per individual and the number of individuals in the population. The pollution is diminished by processes of natural degradation in the environment, and we set up the model so that these degradation processes have a response time of about 20 years (meaning that degradation is equal to 0.05 times the amount of pollution). If you recall from earlier, this response time means that if we cut off the inflow to the reservoir, 63% of the pollution will have been degraded after 20 years. This response time may be a bit optimistic, but remember that we're exploring the general behavior of the system and not necessarily trying to simulate what really happens. The population is dependent on the pollution level in the sense that the death percent is defined as a graphical function of the pollution. The thinking here is that when there is more pollution in the environment, the environment is essentially more toxic and a greater proportion of the population will die as a result of things like cancer and immune system failure. The structure and equations behind this new system are shown in the figure below. Note that here, the Death Pct graph is not drawn, but the input-output values are given in pairs within parentheses. As before, the way to set up this graph is first to connect Pollution to Death Pct with an arrow, then double-click on Death Pct and make it equal to Pollution, and then click on the Become Graph button, which brings up the graph window. Set the ranges of the two axes to match the range of values within the parentheses.
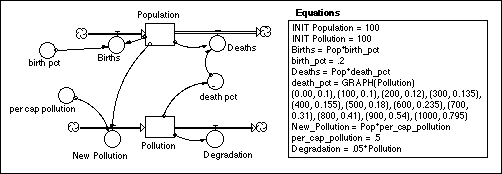
4. Experiments
i) How do you think this new system will behave? This is an especially difficult system to predict the behavior of, as you will see when you run the model. Run the model for 200 years with a time step of 1 year. The only way to predict the behavior of this system is by noting that in a general way, it has the structure of two coupled reservoirs; this commonly results in a tendency towards oscillatory behavior.
ii) Now, let's try to understand the sensitivity of this system to various changes. How does the birth rate affect the behavior? How does the speed (the response time) of degradation affect the system? How do changes in the pollution per capita affect the system? Run through a series of sensitivity analyses to find answers to these questions.
iii) As a final experiment here, reduce the initial amounts of each reservoir to a value of 1 and run the model for 200 years. After making your predictions (will the system still oscillate?), look at just the first 50 or even 75 years of the graph. Could you guess that the system might oscillate based on this limited period of time? The point of this is to emphasize that you can't really know how a system such as this will behave until after the initial period of exponential growth is over, but any time you have this kind of a coupled system, there is the potential for overshoot and collapse or oscillatory behavior. Of course, if you know the parameters of a system well enough to make a computer model, you can predict the future. But in the case of the human population system, we do not know all of the details well enough to construct such a model.
Implications of Continued Growth -- Simple Projections
As of July, 1995, the population of the world was estimated to be 5.733 billion, and the growth rate was estimated to be 1.5% per year. Here, we ask the simple question: what does this imply for our future? Pursuing this question also leads us to the concept of the doubling time for a population.
i) It is easy to make a simple model projection using these two numbers. This is a two-component system, with a reservoir called Population, and a flow called population growth. Draw a connector arrow from Population to population growth and define it as 0.015*Population; then set the initial value of Population at 5.733. Our units here are in billions of people, and the time units are years. Run this model for 100 years, with a time step of 0.5. What is the result? If you run the model, you should obtain a result of around 25.5 billion, but there is an easy way of estimating the result. Under strict exponential growth, where there is a fixed percent of annual growth, the doubling time is defined as follows:
In this equation, 1.5% growth would be entered as 0.015, 10% growth would be entered as 0.1, etc. A simple calculation shows that with a growth rate of 1.5%, the doubling time for the population is 46.2 years. This means that in 92.4 years time, the population will have doubled twice, going from 5.7 billion to 22.8 billion.
Let's return to our projection -- how likely do you think it is? One way to begin answering that question is to think about what the model assumes; it assumes that the growth rate per year remains constant at 1.5% and that there are no limitations to growth.
ii) Now let's make a small addition to the model so that we can keep track of the arable (farmable) land available for each person. It is estimated that there are 1.485 billion hectares of arable land on Earth. Add a new converter called ag land per person and make an arrow from Population to this new converter and then define this quantity as equal to 1.485/Population; this will give us the hectares of arable land per person. What is this value at the end of the 100 years with the 1.5% per year growth rate? Is this a problem? It helps to know that some people say that with present technology, each person needs about 0.5 hectare of land to sustainably provide an adequate, diverse diet. Obviously, we are looking at a very unpleasant future if the human population continues to grow at the present rate. The fact that with the current population, we don't have 0.5 hectares per person is also an important, even shocking sign that we are now bumping into limits to growth. This sign is no doubt especially clear if you happen to be among the one billion people in the world who are malnourished. Unfortunately, it is too easy for those of us with an abundance of food to ignore this sign.
There are also serious question about whether the global economy can expand to provide jobs for this many people. What would this economy be based on? Are there enough mineral and energy resources to fuel this economy? The population growth history resulting from extrapolating the current growth rate also has grave implications for the future of the hydrologic cycle and the carbon cycle. For instance, the projections for future CO2 emissions are based on the assumption that the global population will peak at around 12 to 15 billion rather than climbing to 25 billion; imagine what the carbon cycle would do if we nearly doubled the expected emissions to 40 Gt C/yr 100 years from now.
Limits to Growth
We live in a finite world, which means that the dramatic growth of the past 100 years cannot continue; we will run into a variety of limits to growth. Some of those limits have already been reached or at the very least we are quite close to them, while others have yet to be reached.
Energy resources, in particular fossil fuels represent one kind of a limit; one that could be depicted by a reservoir with essentially no inflow and an outflow that is steadily increasing over time. Why no inflow? Because fossil fuels are formed at such slow rates compared to how quickly we are using them. The net result is a reservoir that is being drained at an accelerating pace.
Another type of limit is represented by mineral resources -- things like metals -- which also have geologically slow rates of formation, and have outflows that are increasing over time as the population grows. The difference is that the drawdown can be slowed by recycling; but since recycling will never be 100% efficient and it also uses a good deal of energy, the reservoir will eventually run down to the point where the metals occur in such sparse concentrations that it is no longer feasible to extract them from the rocks.
Yet another kind of a limit is represented by pollution. As the concentration of pollutants in our environment increases, we face increasingly high costs to deal with the associated health problems and their clean-up. This could eventually provide such an economic drain -- as well as a stress on land and water resources -- that it would impose a limit to further growth. The natural environment has the ability to absorb and render harmless most kinds of pollution, but this sink is not infinite and it therefore cannot handle such high rates of pollution as are presently occurring. Another limit to growth is food, which is discussed in much more detail below.
There is no denying that we can push back some of the limits by coming up with technological breakthroughs and by changing our behavior, but eventually those limits will stand as barriers to continued growth. It is important to realize that we are talking about continued growth, not continued existence. Humans can achieve a sustainable existence on Earth, and in large numbers, and that existence might be very comfortable, but growth cannot continue beyond a certain point. Recognizing where that point is and confronting it will prevent us from experiencing an overshoot and collapse.
Modeling Human Population and Soil Resources
One of the most obvious potential limitations to the growth of the world population is the global reservoir of soil, since it is essential to the production of food. There is a finite amount of arable (farmable) land on Earth, and given a typical productivity level, each person needs something like 0.5 hectares (one hectare is 104 m2 or 2.4 acres) to have a diverse, healthy diet, assuming average yields from the land. Unfortunately, there is only about 0.27 hectares per person at the present population level. This will drop off to about 0.13 hectares per person when the population doubles in the next 40 to 50 years, as it is projected to do. At present, about 20% of the population (1 billion people) is malnourished because of food shortages and inadequate distribution of food. This malnourishment is the cause of over 13 million deaths each year (35,000 per day) and the vast majority are children.
As a means of exploring the problem and the limitations to growth imposed by food and soil, we will create and experiment with a model that represents the system of human population and soil resources. This model will keep track of two reservoirs -- one representing people and the other representing soil. We'll keep track of soil because it is one of the primary controls on how much food can be produced.
The structure of this model is shown in the figure below, followed by the equations, initial values, and graphical functions used in the model. Use the diagram below and the list of equations below as a recipe for constructing this model. As in the previous models, there are several graphical converters included in this model. The reasoning behind different parts of the model is explained below.
The Population reservoir begins with 5.733 billion people -- the global population of 1995, and it has a net growth rate of 1.5% per year, the estimated actual growth rate of the same year. This net growth is the difference between a birthrate of 2.4% per year and a death rate of 0.9% per year. The birth rate is set to be a constant percentage, while the death rate is linked to the life expectancy (currently 62.5 years averaged over the globe), which is in turn defined as a function of the food per capita. This then, is the connection between the population reservoir and the soil reservoir. The death rate is a graphical function of the life expectancy; the precise form of this graph was derived from analyzing data from the World3 model of Meadows and co-workers, which provides the basis for their book Beyond the Limits. In truth, the precise form of this graph is a bit conjectural, but the general trend of this graph is unassailable -- as life expectancy decreases, the death rate must increase. The graph relating food per capita and life expectancy represents the best fit to data (summarized in Beyond the Limits) from a variety of countries around the world, so it is based on the real world rather than a theory.
Before going too far, it is important to discuss our units of food -- calories of grain equivalent. This is different than simple calories ingested by a person since meat products represent a substantial energy loss during conversion from grain that feeds the animals to meat that humans eat. Typically, the ratio is 10:1 for cows and 5:1 for poultry and farmed fish (which is making up in increasing portion of the fish consumed worldwide). So, if you are a normal American and ingest about 2500 calories a day, and 500 of those calories come from meat, then if we take 7.5:1 as an average conversion from grain to meat, you consume (rather than ingest) 5750 calories. But, it is not likely that those other 2000 calories come directly from grains, with no energy lost in the processing. So, in reality, your true food energy consumption, in grain equivalents is likely to be much higher, on the order of 10,000 calories.
The part of the model that keeps track of food is represented entirely by converters rather than reservoirs, in part because of the extremely fast turnover time of the global food stocks, which would force us into a short time step and thus slower calculations. The initial land yield, in calories of food per ton of soil that represents the current yield, is set at 10.92 calories per metric ton of soil. With the present population, this number gives a food per capita value of about 4000 calories (of grain equivalent), which corresponds to a life expectancy of 62.5 years. This land yield is a value that has clearly been increasing over time, as can be seen in the following graph that shows the total grain production for the world since 1950, along with the per capita grain production.

The total grain production has climbed steadily (not exponentially!) and at a higher rate (300% increase since 1950) than the total area under cultivation for grain (which has only increased by about 15% since 1950); thus the yield per hectare has approximately doubled in 40 years. The increase is due to a variety of factors -- increased irrigation, new varieties of plants that are more productive, and increased use of fertilizers, to name a few. The increased yield has been enough to make the per capita grain production increase slightly, which is an amazing feat given that the population has been increasing exponentially. The pattern of increase has faltered since 1990, which may be a sign that the productive potential of the land is being degraded or that the present technology has reached its limits (for instance, some evidence suggests that intensive fertilizer use results in progressively smaller yield increases from year to year -- as if there is a saturation point). But for the purposes of this model, we will assume that the land yield will increase at the same steady rate it has followed for the last 40 years -- this gives what is called the theoretical land yield in the model.
This theoretical land yield (what technology could produce) is then compared with the potential land yield (what the soil will allow) and the lesser of these is then used to calculate the total calories of food that can be produced. The potential land yield is a graphical function of how much top soil there is relative to the starting amount. Here, we are implicitly assuming that the total area of farmed land stays more or less the same; thus a decrease in actual soil mass means that there is less soil per hectare of farmed land, and studies from around the world show that yields are reduced when soil thickness is reduced. In reality, the situation is quite complicated. Land remains in use until it loses so much productive potential that it is not worth the effort to farm it anymore; then it is set aside and will generally begin to heal very slowly. In the meantime, new farmland is brought into production. But of course, all of the best farmland is either currently in use or has been used up, so the new farmland these days is of a lesser quality and has less productive potential; this trend will continue. Another aspect of this problem is that most cities are located near prime farmland and as the cities expand, they consume the best farmland; thus the overall quality of farmland is degrading. But, it is a reasonably good approximation (although definitely on the optimistic side) to say that the total area of farmland will stay more or less constant in the future. If we adopt this assumption, then the total amount of soil can be envisioned spread out in a uniform layer over 1.5 billion hectares; the thickness of this soil layer is then proportional to the potential yield of the land. With less soil, the water-holding capacity of the soil is diminished and the nutrients and supply of those nutrients to plants via microorganisms is also reduced. The exact value of the productive potential of the land is not well known, and would be a devilishly hard thing to figure out, but we optimistically set it to about twice the value of the current yield, or about 20 calories per metric ton of soil. The decline of this potential yield is patterned after observations of yield reductions related to varying degrees of soil erosion from the real world.
As mentioned earlier, the total food production, in billions of calories from grain is obtained by taking the smaller of the two yields (theoretical -- what technology can do-- and potential -- what the land will permit) and multiplying it by the total amount of soil. This total food amount is then reduced by a factor of 30% to account for loss and waste in the harvesting and distribution processes, and then divided by the population to give the food per capita in calories per person. The 30% waste/loss value is the present estimate and is shockingly large; if it were reduced to zero, there would be no practically no malnourishment problem in the world. A large part of this waste problem is that so much of our food is produced so far from where the concentrations of people are. If more food was grown and consumed locally, this waste could be greatly diminished and there would be the added benefit of having people be more closely connected to the production of their food.
The soil reservoir has an inflow that represents the process of new soil formation. The flow is here set to a constant rate, such that the entire soil reservoir would be replenished in 500 years. This is a very slow process; it amounts to an increase in soil thickness of just half a millimeter per year. The soil reservoir also has an outflow process that represents soil erosion, defined in the model as the percent soil loss multiplied by the amount of soil left in the reservoir. The percent soil loss is in turn defined as the product of the initial percentage of soil loss (about 1% per year at the present time) and a parameter called intensity multiplier, which is a graphical function of the food shortage per capita. The idea here is that when food becomes more scarce, people will become more and more concerned with trying to produce more food; they will use the land in a more intensive way. The more intensely used the land is, the more susceptible the land is to increased rates of soil erosion. This is simply because the immediate concerns will take precedence over the longer-term needs, which would be better served by more conservative use of the land. The graphical relationship between the food shortage per person and the intensity multiplier is purely speculative, but it is set up so that at the beginning, the intensity multiplier has a value of one and thus has no effect; when the food per capita drops to 2000 calories below a minimum acceptable value, the intensity multiplier goes to a value of 10. It is worth pointing out that when the food shortage is this severe, life expectancies will drop to around 30 years, and the death rate will skyrocket to nearly 25% per year -- this clearly represents a very severe condition, and under these circumstances, increasing the soil erosion by a factor of 10 is probably a conservative estimate. The minimum acceptable food per capita, called min food pc in the model, represents the level of food supply at which people begin to take major action in order to attempt to produce more food. To begin with, this value is set at 4000 calories per person, the present day value (although people are starving, we actually do produce enough food, and the suffering of those whose starve is apparently, we must unfortunately admit, not capable of motivating the world to do whatever it takes to produce more food).
It should be clear from the above discussion of the construction of the model and the reasoning behind it that this model is full of speculation, but in most cases, that speculation is fairly optimistic, favoring the idea that more food can continue to be produced. This means, though, that the results of the model are not to be taken as real predictions of what the future holds. For instance, many other factors go into the determination of the life expectancy, and an equally large number of factors go into determining the birth rate; these additional factors are not considered here. For a more thorough treatment, you are encouraged to look at the World3 model of Meadows and others, described in their book, Beyond the Limits.
5. Experiments
With this model, we will explore a variety of possible futures -- investigating the implications of various assumptions about how we will respond to the food supply of the future. The experiments are a bit different from others in this book in that there is no steady state that will serve as a control (although a steady state is clearly the most desirable condition for this system). Instead, our control will be the resulting behavior of the initial model, described in the equations above, which we can think of as the "business-as-usual" case.
5.1. Business-as-usual
Before running the model, try to make some predictions about how this system will evolve over the next 200 years. You might try to imagine this history in terms of the population reservoir, the food per capita, the life expectancy, and the soil reservoir. After you've made some careful predictions, run the model for 200 years with a time step of 1.0 years, using the Euler method of integration. Can you explain why the model behaved as observed?
Remember that this is not a highly constrained, quantitatively significant model. There are enough assumptions and simplifications that we should think of this model as giving us a chance to explore the consequences of these assumptions. This is not a prediction of what will really happen!
5.2. Reducing Waste
Now, let's investigate what might happen if we can find ways to reduce the waste. This could happen through some advances in the storage and distribution of food -- part of the solution might involve more localized production and distribution of food. This might mean, for example, that people living in Minnesota learn to live without as much fresh produce in the winter and that farmers in Minnesota begin to grow things other than just soybeans and feed corn. This would undoubtedly lead to a rise in food prices, but most Americans could easily adjust by eating less, which would also be good for their health, thus their quality of life might actually improve.
To investigate the effects of reducing waste, let's do a sensitivity analysis in which we run the model with different values for the waste percentage. Select Sensi Specs from the Run menu and then select Waste from the Allowable column and use the >> key to send it to the Selected column. Set the value in the # of Runs box to 4, then click on Waste in the selected column, make sure that variation type is set to incremental, and then make start at 0.3 and the end at 0.0. Next, click the Set button and you'll see what value of Waste will be used in each run. Make sure the Sensitivity On box is checked, then exit this window by hitting the OK button. In making predictions here, think about what will happen to each of the following model components: Population, Soil, food per capita, life expectancy. Set up four different graphs, one for each of the above mentioned components, and make sure the Comparative button is highlighted (this will limit you to plotting only one thing on each graph). Run the model for 200 years, with a time step of 1 and study the results carefully. Does reducing waste alone really help in the long term? What does this tell you about which parts of the system are the most critical if our goal is a sustainable, i.e., steady-state population?
5.3. Increasing Technology
The model already assumes that technological improvements in the way food is produced will continue into the future as they have in the past 50 years, during which time steady progress was made. But, let's see what happens if we assume that the rate of technological improvements will increase, occurring twice as fast as in the previous 50 years. This might reflect a much greater focus of intellectual and financial resources on the matter of agriculture. To do this, double-click on the converter called theoretical land yield and change it to:
theoretical_land_yield = initial_land_yield * (1 + (0.04 * time))
Before running the model with this more optimistic view of technological advances, think carefully about what will happen. As before, run the model for 200 years and compare the results with the business-as-usual case. What can you conclude about the idea that technology will save us? Remember that here, we have placed some clear limits on what we mean by technological improvements.
5.4. Reducing the Minimum Acceptable Food Per Capita
According to one study, the food produced in 1990 could have fed 5.9 billion people on a subsistence-level diet, even after accounting for a waste of at least 30%. That would mean that no one was starving, unlike the present situation. That same food could only sustain 2.9 billion people on a European-quality diet (fewer still on an American diet). As food per capita decreases, and more of the world's population suffers from malnutrition, it will be helpful if people such as those of us in the high-consumption, overweight countries of the world learn to modify our diets; the resulting food savings could then presumably be passed on to those less fortunate, bringing their diets up to a healthier level. In doing this, the goal would be to even out the distribution of food calories with the world average a bit lower than it is at present. One way of doing this is by reducing the amount of beef and pork consumed. Beef has about a 10:1 ratio of grain calories input to calories of meat produced, pork is about 7.5:1, whereas poultry and farmed fish (which may soon replace natural fish since most fisheries are being depleted quite rapidly these days) have a ratio of around 5:1. So if we eat more farmed fish and poultry and less beef and pork, we will reduce our overall consumption of primary food calories and we will probably be healthier.
To explore the implications of reducing the minimum acceptable food per capita, set up a sensitivity analysis (you should be somewhat familiar with the procedure for doing this in STELLA -- imitate the steps described in experiment 2 above), varying the min food pc from 4000 to 3000 in three steps. First, make some careful predictions about how the system will behave, then study the effects of these changes by plotting a variety of comparative graphs plotting Population, Soil, food per capita, life expectancy, and other parameters that you feel are important. How do the results of these experiments compare with the other attempts to improve our future (the previous two experiments)? Can you explain why changing this parameter led to the observed behavior of the system?
5.5. Changing Soil Erosion
Soil erosion is presently a very serious problem around the globe, with estimates ranging from 1% to 2% loss per year -- as much as 75 billion tons of topsoil are lost each year. Part of the problem is that most of the erosion does not occur through the formation of dramatic gullies; instead, it occurs through sheet erosion that removes nearly uniform layers of soil from the surface (both wind and rain are the agents of this erosion). An intense overnight storm, for instance, might strip away one millimeter of soil (this is about how much might form in two years), which would never be noticed. Thus, soil erosion is the kind of insidious problem that is likely to sneak up on us and it is difficult to generate too much concern for this problem. To get an idea of how soil erosion effects this system, we will do two separate experiments here; one in which we change the initial amount of soil erosion and one in which we change how soil erosion changes with increased stress on the food supply system.
a) For the first experiment, we will explore the effects of changing the initial amount of soil erosion -- the percentage of soil loss that is thought to occur at the present time. Because it is so hard to estimate the global magnitude of soil erosion, there is considerable uncertainty about how much soil erosion is actually occurring. In the Sensitivity Specs window, set the initial pct soil loss to vary from 0.01 to 0.02 in three steps. After making some predictions about how the system will respond, study the effects of these changes by plotting a variety of comparative graphs of Population, Soil, food per capita, life expectancy, and other parameters that you feel are important. Use the Business-as-usual scenario as the control for this experiment. You may need to run the model for 400 years in this case, with a time step of 1.0.
b) For the next experiment, we will leave the initial percent of soil erosion at 1% and instead alter the graph that relates the magnitude of the food shortage to the intensity multiplier. This intensity multiplier, as you can see, affects the amount of soil erosion -- it acts as a multiplier on the rate of soil erosion. Initially, this graph is set up to reflect the assumption that as food becomes more scarce, people will place the highest priority on producing the greatest amount of food as quickly as possible, which is easier if you ignore measures that prevent soil erosion. The net result is to increase the loss of soil. (On the other hand, if there is no severe food shortage, this graph yields an intensity multiplier that is less than 1, which will reduce soil erosion.) In this experiment, however, let's investigate what happens if we assume that we will never abandon efforts to prevent soil erosion (but we will not lessen erosion below its present rate). We can incorporate this assumption by modifying the graph that determines the intensity multiplier so that for all values of the per capita food shortage, the intensity multiplier remains at 1.0. After making this change, predict how it will affect the system, then run it for 200 years, comparing the results with those of the initial, business-as-usual scenario.
5.6. Increasing Soil Formation
As mentioned earlier, we assumed that on average, the soils of the world take 500 years to form; we used this to set the rate of soil formation to a constant value. What if this estimate is off? This is a fair question to investigate since the 500 year figure is simply an estimate based in part on carbon-14 dates from a variety of soils -- perhaps the soils sampled do not accurately reflect global averages. In this experiment, we will change the rate of soil formation from 3500/500 to 3500/300, corresponding to a 300 year period of soil formation. How do you think this will affect the system? Make your prediction, then run the model for 200 years and compare your results with those from the business-as-usual scenario. What is the main effect of changing this parameter?
What Can Be Done?
One of the biggest questions of our times is whether we can stop the exponential population growth before we overshoot our sustainable limit. Part of the problem is that we do not know precisely what that limit is, and it may in fact change according to technological developments. The other part of the problem has to do with developing reasonable, effective, acceptable methods for reducing population growth -- how can it be done quickly, humanely, with respect for people. Concerning the first part of the problem, there seems to be abundant evidence that we are in fact approaching the carrying capacity of our environment. If we act on this information with intelligence and speed, we can almost certainly prevent the kind of tragedy that is associated with an overshoot and collapse scenario.
The experiments you've just completed show that improving the efficiency of feeding ourselves (we get by with fewer calories per person) and reducing soil erosion are both important in achieving a sustainable population. But, in all cases where the model approached a steady state, it did so by increasing the death rate, which means that the average life expectancy decreased. This is akin to saying that the quality of life was reduced. But, we did not consider the other logical alternative -- limiting birth rates.
If our goal is to limit population growth, we know that we can either change the death rate or the birth rate -- which is more humane? I think most people would agree that it is more humane to limit the birth rate, depending of course on how this is achieved. Mass sterilization and forced abortions would of course do the job, but they do not hold promise for sustainability because of the resentment they may create, and they do not address the cause of high birth rates, so they are attacking the symptoms and not the cause. Before pursuing the matter of birth rates further, we should verify that indeed, growth rates are closely related to birth rates, which would support the idea that lowering birth rates would lower growth rates. The graph below plots the birth rate vs growth rate for a selection of 44 different nations that span the globe and represent a range of economic conditions.
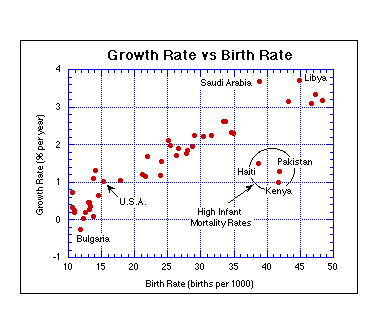
This good correlation between these two means that it is reasonable to assume that by lowering the birth rate, we would also lower the growth rate -- not exactly a shocking conclusion.
So what is the cause of high birth rates? In the past, some people have figured that lack of information and access to birth control were the main factors responsible for high birth rates, and so there was an effort to provide contraceptives and family-planning clinics to countries with very high birth rates. But, while these services and information clearly enable couples to have fewer children, they do not make couples want to have fewer children. Thus, these efforts were still not attempting to address the underlying cause. Why do couples want to have many children? That is the question we seek an answer to.
One reason to have many children is to provide for you when you are old and unable to work and get your own food. This is a reality in many countries, and the only solution is to create a program of old-age pensions. But, such a program requires money from some source. Who will pay? Who can pay? Clearly, many of these countries do not have the financial resources to pay, even if the political will existed to start such a program.
Another reason why couples in some countries have many children is because the infant mortality rate is so high; if a couple wants to be assured of having three grown children, they may feel that they need to give birth to six or eight. Since they are not operating with a clear knowledge of what the infant mortality rate is, the tendency is to over-produce. The solution to this is simply better health care. But, is it possible that relatively "poor" (in terms of money) countries can acquire good health care? It seem difficult when you look at how much we spend in the US on health care. Surprisingly, a "poor" country like Cuba has such an effective health care system (they concentrate on prevention rather than expensive cures) that their infant mortality rate is about the same as in the US So, it can be done. The graph below shows the "wealth" of a country, the Per Capita Gross National Product (GNP) vs. the infant mortality rate (deaths per 1000 live births) for the same set of 44 countries.
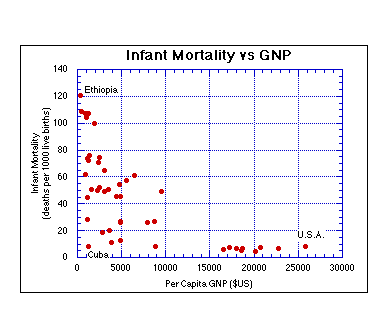
the message here is that you don't have to be a wealthy country to have a low infant mortality rate, but it helps. But, it appears that wealth of the type we have in the US is not necessary -- we might expect the same mortality rate with a per capita GNP 40% lower.
Another reason to have children has to do with creating a sense of power and bringing in money. This attitude prevails in cases where mandatory education from 6 to 16 does not occur; when kids are not in school, they can work, and even though they receive low wages, 6 or 8 kids can bring in a good deal of money. But, requiring kids to go to school removes their wage-earning potential, and they become expensive; when they are perceived as expensive, they are less desirable. A beneficial side-effect is that when child-labor ceases, the average wages in a country go up. Universal education is therefore an excellent means of addressing one of the root causes of high birth rates, and it is relatively inexpensive -- it could be achieved in most countries by redirecting a tiny fraction of the money spent for military purposes. Cuba and Zimbabwe are examples of countries that have succeeded in lowering their growth rates and part of their success is attributed to universal schooling.
Education of women in particular is another way of addressing one of the causes of high birth rates, especially when that education is geared towards preparing them to take paying jobs. If more women are actively bringing in money, there is a powerful, direct economic incentive to have fewer children --too many children then pose an obvious burden, with negative economic consequences. In non-rural societies, basic education is generally necessary to enter the work force, so we might take the percentage of women who are literate as a measure of the percentage of women who are educated and capable of taking on paying jobs. The graph below plots the female literacy rate vs the birth rate, for the same set of 44 countries.
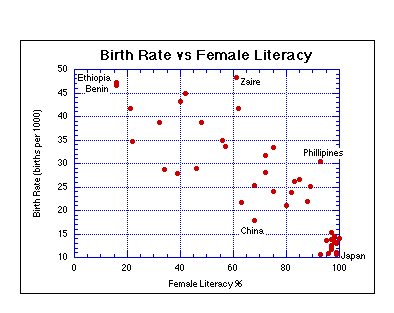
This is a surprisingly strong correlation considering the number of factors that contribute to the birth rate. One way of interpreting this graph is that if more women are educated and thus provided with the means of taking a paying job, they will do so, and as a result they have fewer children, presumably because they (and their spouses) see the economic disadvantage of having too many children. We may then wonder about the cultural and economic barriers to creating this kind of an educational program. If we look at the female literacy plotted below against the GNP for these countries, we see that "wealth" is not necessary in order to achieve female literacy, but an intermediate level of wealth seems to guarantee a high rate of female literacy.
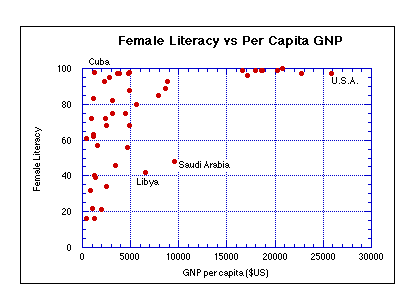
Or perhaps you might argue that achieving female literacy tend to lead to a higher GNP because you have more people working and thus an expanded economy. In either case, the thing to emphasize is that by raising the status of women, by inviting them to participate in the job market, birth rates, and thus growth rates go down, which is what we need.
What about cultural barriers to improving the status of women? They certainly exist, but of course they exist in countries where women are regarded as inferior beings, where men have all the power. Does this mean that people from Western societies should not do everything they can to improve the status of women in these countries? As an interesting analogy, consider that in Canada, not too long ago, women were not legally recognized as persons, and it took the British government to persuade the Canadians to admit that women were regular people, in a legal sense. These days, people are wary of cultural imperialism, and for some very good reasons, but the oppression of women is not something that should be accepted. We do not, in the western world, at least to hear us talk, tolerate the oppression of one group of people (nation) by another, so why should we tolerate the oppression of women? Also, we must all ask ourselves if we can really afford not to do everything in our power to bring the human population system under control.
Given the array of plots shown above, it will come as no surprise to look at a graph plotting the birth rate vs the GNP for this set of countries.

Not surprisingly, we see that the "wealthier" countries tend to have lower birth rates (and also lower growth rates). By now, you should have a pretty good sense that there are many factors behind this correlation. But, it does serve to bring up an important concept that is sometimes called the demographic transition, which is a transition that occurs during the economic development of a nation. When a nation is in a pre-industrial state, both birth rates and death rates tend to be very high, growth rates are low and so are populations. As industrialization begins, death rates drop first because they respond very quickly to health care and improvements in living conditions, and birth rates tend to lag behind a few generations. It is this gap that creates explosive population growth, and it does not stop until after the industrialization is well underway. Here, we can think of the GNP as being an indication of how industrialized a country is -- "wealthier" countries have passed through the demographic transitions and their populations are fairly stable, as indicated by their birth rates. If this concept of demographic transition as the control of population growth is right, then the above graph is a bit frightening since you can see that many countries of the world have apparently not passed through this demographic transition yet to the point where they are "wealthy" and have stable populations.
So, we might conclude that one of the best things to attempt, in order to bring about a stabilization of the global population is to usher as many countries as possible through the demographic transition as quickly as possible. This amounts to massive, and thoughtful, economic assistance. But, if we want to achieve this goal and not ruin the environment, the economic development of the "poorer" nations will probably require that the few wealthiest nations stabilize or even scale back their own economies. This means that we in the Western world will have to give up our highly consumptive lifestyles and be content with more modest levels of wealth, with fewer luxuries. This also means that our economic system (which is really a reflection of our society) will have to abandon the notion that growth is the ultimate good. To most economists, it is a heresy to suggest that growth cannot continue infinitely, but if you are familiar with the dynamics of systems, you will immediately recognize that continued exponential growth cannot be sustained indefinitely. Instead, we will have to re-focus our thinking and redefine our goals so that a stable, sane, equitable economic system results. If this economic transformation is done with some thought and a minimum of greed, chances are good that we will end up with a healthier, happier society. This seems like a small price to pay if we are to avoid the kind of suffering that would accompany an overshoot and collapse of the global population.
A Few Closing Thoughts
An optimistic view of things would suggest that as the human population approaches the actual carrying capacity, there will be sufficient signals and we will collectively act on those signals in such a way as to prevent an overshoot and collapse from occurring. As an example, those signals could come in the form of increasing prices for natural resources, which wood encourage a reduction in use through conservation, recycling, and increased efficiency. But, since the fossil fuels we rely on for most of our energy are produced as incredibly slow rates, we cannot achieve a steady state condition for these energy resources. Thus, we will ultimately have to get all of our energy from sustainable sources such as solar, wind, and nuclear sources (nuclear fusion rather than fission, whose waste products are too problematic). We have a nice example of how this can work in the case of the energy crisis of the 1970's -- rapid changes occurred in response to the decrease in availability of petroleum. Unfortunately, most of these changes were reversed shortly after, once the flow of oil from the OPEC countries to the US was continued. Nevertheless, this example does serve to show that we can change if we are convinced that we must, if it is economically favorable to change.
Another signal that we are near the carrying capacity may come in the form of increased problems and costs arising from the effects of pollution in our environment. Presumably, once we are spending a large-enough portion of our money dealing with the problems of pollution, the less we will pollute. But, in this case, the problem is that if we stop pollution today, its effects won't be gone tomorrow -- the problems of pollution persist for decades.
A similar example involves soil, which is essential to food production. Human land-use is resulting in a great deal of soil erosion -- it vastly exceeds the rate of regeneration of soil; thus there is a net loss. As the global pool of soil is diminished, so is our ability to produce food. Soon, this problem will grow to the point where we take action to stop soil erosion and degradation, but at that point, we will have to feed the world from the remaining soil -- it does not form quickly enough to replenish the reservoir on a human time scale. In this case, we will have to hope that tremendous gains in sustainable agriculture occur so that we can go on feeding the world.
In the above three examples, we can react to the signals and change, but can only continue on in a sustainable state if we make major changes in the way we operate. Some of these changes require technological advances that are beyond our grasp at the present; thus we need tremendous faith in the ability of people to make the necessary break-throughs and discovery (this means that education is a huge priority). But, we cannot simply trust that technology will save the day, allowing us to continue living our lives as we do at the present time. Realistically, we have to change; we have to become less consumptive, more responsible, and more understanding of our role in the global system.
A good portion of the above discussion is aimed at understanding what the carrying capacity of the human ecosystem is, and what kinds of limits define that capacity. These are important concepts to the extent that they give us some sense of what we might expect in the future. But, perhaps the most important question of all is this -- what kind of a future do we want? Do we want the system to find its carrying capacity and stay there? Or do we want to stabilize population well below the limit? If we choose the former (which is essentially the choice to take no real action), it is likely that we will have at least 3 times as many people as at present. What would your life be like then? Where would you go to find solitude? Where would you go to study, enjoy, and meditate upon the natural world? We can avoid a world with 15 billion people, but we have to make some conscious choices that entail some sacrifices for those of us in the wealthiest nations -- we have to choose quality of life over quantity of life. This is a huge challenge, and it seems to me that the starting point is to educate ourselves about where we are headed.
Slipping into Chaos
This seems like a good chance to digress into the realm of chaos, not because I wish to emphasize how chaotic the world is, but rather because one of the equations we've been using in this chapter exhibits chaotic behavior under certain conditions. The system structure of interest here is the one shown in the figure below.
We could simplify the above system a bit by turning the graph into a simple equation for a straight line. Looking at the above graph, we can see that:
With this expression, we can rewrite the equation for Deaths so that it becomes:
We can then write a simple equation that expresses the whole system:
where P is the population and a and b are constants that are related to the birth and death rates. This is sometimes called the logistic equation or the Verhulst equation after the mathematician who applied this equation to the study of population dynamics. Here, we will consider a simpler version of this equation, one in which the two constants are equal to each other, leaving:
This kind of a differential equation is called non-linear because P is squared; in general, non-linear differential equations are susceptible to some very interesting behaviors, as we shall see below. The structure of this system is very simple, as shown in the figure below.
Construct this model and run it for 50 years (we will arbitrarily say that our basic time unit is one year, but if this model were to represent a population of bacteria, our time unit might be more like an hour), plotting the population. You should see a vaguely S-shaped growth curve resulting from this model, as shown in the graph below.
Nothing complicated or unexpected about this. But now we will explore some extreme conditions, where the factor r grows very large, corresponding to birth rates from 200-300% per year. To begin with, do three runs of the model varying r from 2 to 2.25 to 2.5. In each of these cases, run the model for 100 years, with a time step of 1.0. You will see that for values of r=2.0 and r=2.25, the population oscillates back and forth between two values -- we call this a period two oscillation. But at r=2.5, we see a period four oscillation. This is strange behavior, but it still seems fairly orderly. Next, change the value of r to 2.58 -- this should give you a period eight oscillation. Now, increase r to 2.7 and see what happens. You can study the resulting graph for a long time, but you probably cannot pick out a true repeating pattern. At this point, the behavior has become chaotic. Next, try increasing r to 2.83 and run the model, studying the behavior out past about 50 years. Surprise! The system seems to have calmed down, finding a period two oscillation. But then increase the value of r to 2.9 and try again. Surprise! Back to chaos. You see that we have a very complicated, apparently unpredictable system that comes out of an incredibly simple equation.
To explore this equation further, we will set up a sensitivity analysis to investigate the behavior of the system of many values of r in a single graph. Go to the Sensitivity Specs window and set it up to do 30 runs, with r varying from 1.8 to 2.8. Now we're going to add a new feature to the model that will make it easier to study in a graph and we're doing this because of the observation that in some cases, the system seems to require a bit of time to "settle down". So, create a new converter and label it P and draw a connector arrow from the Population reservoir to P. Define P as follows:
P = IF time>25 THEN Population ELSE 0
This will effectively ignore the values before 25 years, giving the system a chance to settle down. Next, set up a comparative scatter graph that plots values of r on the x-axis and P on the y-axis. Then run the model for 75 years with a time step of 1.0 and sit back and watch what happens. We are creating what is called a bifurcation (a bifurcation is a place where something splits into two different strands) diagram -- it shows the values of r at which the system changes behavior. You should see something like the figure below:
In this graph, you can easily see where the transition from a stable, non-oscillating behavior switches to a period two oscillation and then to a period four oscillation and so on, but it is clear that as we progress to higher values of r, the changes come more rapidly. If we were to do enough variations of r, we would have a very complete map of all the bifurcations of the system, and the amazing thing is that with such a map, we could see that it is self-similar at many scales of observation. That is to say that if we magnify our view of one of the more complex regions and stretch out the x-axis, we would find that each bifurcation is geometrically similar to the one from period two to period four that we saw on the larger scale. This self-similarity is a characteristic of a fractal.
What is a fractal? It is a geometrical form that is characterized by some interesting properties, but it is perhaps easiest to quickly grasp what a fractal is through a few examples. A commonly used example of a fractal is a coastline, which, viewed from an airplane, has a certain variability relative to the length you can see; but when you change your point of view, kneeling along some portion of that shoreline, you see the same approximate variability relative to the length that is captured by your field of view. If you were to measure the length of the coastline using a variety of measuring devices, each with a different length, the length of the coastline would vary systematically as a function of the unit of measurement and if you plot the length of the coastline vs the length of your different measuring devices, the slope of that curve gives what is called the fractal dimension of the coastline. Another example of a fractal is a sugar maple tree, which has a trunk that bifurcates into a couple of main branches, which in turn bifurcate into smaller branches and so on until you get to the leaves, and then you see the same kind of bifurcation geometry continuing at much smaller scales. You can look at this tree from a distance or up very close and you see the same kind of geometry -- it is self-similar on a variety of scales.
Getting back to our bifurcation diagram, if we see it as a fractal, the incredible thing is that it implies that there is a definite order or organization to what we call chaos. The other important thing to note from the bifurcation diagram is that the bifurcations are abrupt. This means that if you are right at the edge of a bifurcation, the tiniest change in the value r can produce a wholly different system behavior. In other words, there are thresholds that are very abrupt and once they are crossed, the system is very different. This sensitivity is what made one of the first people -- a meteorologist named Edward Lorenz -- to confront chaos mathematically pose the question, half-jokingly, of whether the flapping of a butterfly's wings in Brazil cause a tornado in Texas.
Another view of the kind of order that underlies this system can be seen by exploring our model of the logistic equation a bit further. In this case, we will set up another system that produces a random variation in the population to provide a contrast with the logistic equation. First add a new converter called Last Population and define it as follows:
Last Population = DELAY(Population, DT)
This function means that Last Population will always have the value of Population during the previous time step. Then create two more converters, calling one X and the other Last X. X and Last X will be defined as:
This will make X vary through time randomly between 0.3 and 1.3, and Last X will have the value of X during the previous time step. Now, if we run the model, we can see the difference between a chaotic function and a random function, first plotted as they vary over time:
From the above graph, you can see that the chaotic function seems to be a bit more regular than the random function, but without a great deal of experience looking at random and chaotic behavior, it is difficult to tell what is random and what is chaotic from this type of graph. But, when we look at the data a different way, the task of differentiation is much easier. Here, we plot the Population vs the Last Population, and X vs Last X:
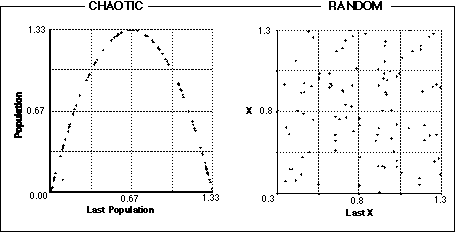
At first, the order of the chaotic system is quite surprising, but when you look at the equation that drives this system, you see that it has the form of the equation for a parabola (y = ax - bx2). In this way, we see that there is a clear mathematical relationship between the population at any one time and the previous population. You can predict that at all points through time, the successive populations, plotted together, must fall on this parabola, but you can't really be any more precise than that.
Perhaps it has crossed your mind by now that there is an apparently frightening implication of this chaotic behavior to the extent that many populations, including our own, are described by this logistic equation. Does this mean that all populations have the potential to slip into chaotic behavior if we cross over a threshold?
Here, it is important to realize that by using such a large time step, we were moving very far from what might be called a continuous solution to the equation; one in which the calculations are done over very small increments. In nature, many populations grow in a more continuous fashion -- individuals are constantly dying and being born. So, let's see what happens if we solve these equations with a very small time step. Using the model above, decrease the time step to 0.1 years, and run it for 25 years, with r set at 3.0 -- you should e see a very different behavior, illustrated by the dashed line in the graph below:
The dashed line representing the more continuous solution (time step set at 0.1 years) contrasts sharply with the jagged, solid line representing the discontinuous solution (time step of 1.0 years). The difference is quite striking, and you might even say reassuring to the extent that most populations evolve in a more continuous fashion.
Not all systems of equations that have the potential for chaos show this markedly different behavior depending on how continuous the solution is. In general, a complex system, say one with three reservoirs and coupled inflows and outflows, will behave chaotically regardless of the time step. An example of this is provided by the equations named after the meteorologist Lorenz, who did some of the earliest work on chaotic systems. These equations describe the flow of a fluid in three dimensions. In the system shown below, the reservoirs, X, Y, and Z represent the three-dimensional position of some part of the fluid at any time.
The equations and initial reservoirs values are given below:
- Reservoirs:
- INIT X = 1
- INIT Y = 1
- INIT Z = 0
- Flows:
- delta_X = a*(Y-X)
- delta_Y = (b-Z)*X-Y
- delta_Z = X*Y - c*Z
- Converters:
- a = 10
- b = 40
- c = 8/3
If you run the model for 15 time units, with a time step of 0.005, the system evolves as shown in the graph below:
Here, as with the logistic equation, you can glimpse some kind of order to the behavior of this system, but you can't find a nice repeating pattern. Once again, we can see some more of the underlying order in another type of plot, here looking at X vs delta X, where delta X is basically the change in position in the x-axis of space.
This system seems to behave as if there were two centers of gravity that control the orbit of some particle in space. These centers of gravity are called attractors in mathematical language and they are characteristic features of classes of non-linear differential equations. The more interesting thing is that these equations represent some of the physics of fluid flow that underlie the weather, which means that weather may be an inherently chaotic phenomenon (part of the reason that people have such poor luck in forecasting weather), but it is not a random phenomenon -- it has attractors that control it with a certain range.
Key References and Readings on Population Growth:
Further Reading on Chaos: