Introduction
Introduction
Anyone who lives near a river that experiences periodic floods understands the importance of understanding the dynamics of water flow in a watershed -- the area drained by a particular stream or river. Every year, floods are responsible for significant loss of life and property damage despite the efforts to control flooding through the construction of dams. Floods are regular occurrences along most rivers -- they are an important part of the natural stream cycle -- but most people consider them unnatural and seem to have little memory of the frequency of flooding in the past. So, people continue to develop the floodplains of rivers (the floodplain is the broad, flat plain adjacent to a river that is frequently occupied by the river during a flood). The temptation to inhabit floodplains is quite strong; they are level, fertile tracts of land, close to the water table in most areas and thus ideally suited for agriculture. It is unfortunately typical that many people have had the arrogance to ignore the natural operation of this system and instead imagine that the floods can be subdued and controlled and that the costs associated with this task (and its failures) do not warrant a consideration of alternative ways of dealing with flooding. This theme of trying to control and dominate the natural world runs throughout the history of the "civilized" world, and history of full of sad stories of the consequences. But, our purpose here is not to analyze history, but rather to analyze the behavior of this system, with the idea in mind that a better understanding of the system can provide a better basis for dealing with rivers.
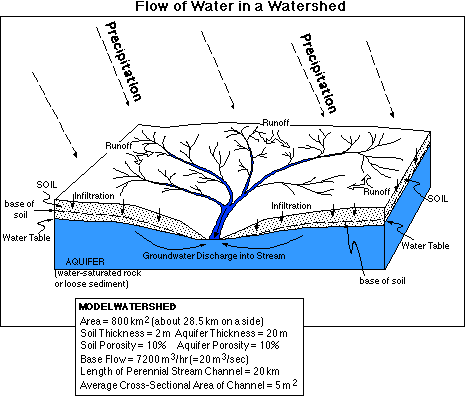
To begin with, let's consider the form and appearance of a typical watershed, illustrated in the figure below. Included in this figure are some of the physical characteristics of a typical watershed, one we will create a model of and experiment with.

If we think about it from a systems standpoint, the amount of water in a river depends on the inputs and the outputs. The inputs are water flowing over the surface water seeping in through the bed of the stream from the soil and/or groundwater (although in arid regions, this second inflow is actually an outflow; the stream lies above the water table and loses water to the soil and ground water). The flow of water from soil and ground water sources constitutes the base flow of a stream and most streams in the eastern half of the US are maintained by this ground water and soil water contribution. Water leaves the river by flowing down the channel; this rate is controlled by things like the gradient of the stream, the roughness of the stream bed, and the shape of the channel. The shape of the channel is important since it determines what portion of the flowing water is in contact with the stream bed and can thus be slowed by friction associated with the rough surface of the stream bed.
The inputs -- runoff and ground water and soil water flow -- are themselves controlled by a variety of physical characteristics of the watershed, the soils, the underlying aquifer, and the weather. The processes that affect these inputs will be discussed next, as we consider ways of defining them in our model. But first, let's go through the process of converting the information in the above figure of a watershed into a STELLA model.
Reservoirs
River Water
The first question to consider is what reservoirs we need to include. One reservoir can represent the water contained in the network of stream channels that experience year-round flow in the watershed (this is undoubtedly a small fraction of all of the channels within a watershed). As seen in the figure above, we will assume here that this channel length is 20 km and with an average cross-sectional area of 5 m2, we have 100,000 m3 of water residing in this reservoir -- this gives us the initial amount.
Ground Water
Another reservoir will represent the ground water stored in the aquifer below the water shed. In many cases, the aquifer may extend far beneath the surface, but here, we are more concerned with the part of that aquifer that feeds water into the stream; this is likely to have a thickness roughly equivalent to the amount of topographic relief in the basin. To begin with, we will use an aquifer thickness of 20 m, which, combined with a porosity (percentage of pore space by volume -- effectively the space that could be occupied by water) of 10% and a watershed with an area of 800 km2, gives an initial volume of 16E8 (or 16 x 108) m3 -- a lot of water.
Soil Water
The soil, star of our previous model, makes another appearance as a reservoir. With an average thickness of 2 m and a porosity of 10%, this gives us a volume of 1.6E8 m3 at capacity. To begin with, we will have the soil reservoir be half saturated, or half of its capacity; this gives an initial volume of 8E7 m3.
Surface Water
Also making a return appearance in this model will be the water occurring as a thin layer at the surface, present when the rate of precipitation exceed the rate of infiltration into the soil (also during the winter, but we're not dealing with winter here). To begin with, this reservoir will have a value of 0.
Flow Processes
Precipitation
The total amount of rain fall on the surface in our watershed is equal to the rate of rainfall times the area of the watershed. We will always assume that the rainfall is uniform, but given the size of our watershed, it is possible that significant variations might occur in some storms. The rainfall rates will be specified in units of cm/hour, so one hour is the basic time unit for the whole model (a far cry from the one month time unit used in the last model). To provide some idea of the upper range of rainfall rates we might explore, the table below gives some of the record maximum rates.
MAXIMUM OBSERVED RAINFALLS Quantity Time Period Rate cm/hr 2.0 m 24 hrs 8 1.4 m 12 hrs 12 1.0 m 6 hrs 16 0.4 m 1 hr 40 7.5 cm 1 min 450 data from Barry and Chorley, 1992
Infiltration
When water falls on the surface, it will either runoff over the surface, or it will infiltrate into the soil. The rate of infiltration varies on such things as the composition and structure of the soil and how much water is already in the soil. Soils have the tendency to allow rapid infiltration when they are undersaturated, but this rate drops off considerably when the soil is saturated. At the point of saturation, the rate of infiltration will be at some minimum value; here that value is set at 1 cm/hr, while the rate when the soil is empty goes up to 8 cm/hr. The value of 1 cm/hr is typical for sandy-silty soils; a very sandy soil may have a value of 2 cm/hr and a clay-rich soil may have a final infiltration rate of 0.1 cm/hr. As in the previous model, we will define the flow rate or velocity (in cm/hr) as a graphical function of the soil water. This velocity is then multiplied by the area of the watershed to give the volume of water that is allowed to infiltrate during each time step.
We will use a graph relating the infiltration rate (cm/hr) to the amount of soil in the water, just as we did in the soil water model (go here for a more detailed explanation).
Percolation
Although percolation and infiltration are very similar words, we use percolation here to refer to the transfer of water from the soil to the deeper aquifer -- the ground water reservoir. This rate of transfer is very low when there is little water in the soil, and rises to some maximum value, which is set here to be equal to the infiltration rate when the soil is saturated. This means that when the soil is saturated, the rate of infiltration will be equal to the rate of percolation. Percolation, like infiltration, is not only a function of the amount of water in soil; it is also dependent upon the texture (mixture of and, silt, and clay in the soil) and overall porosity. Because of this, these two processes should not be altered independently.
As with infiltration, we will utilize a graph to define the relationship between the soil water content and the rate (cm/hr) of percolation.
Discharge
Within the watershed, below the surface, water flows laterally through both the soil and the deeper aquifer from regions of higher elevations to lower elevations, where streams are located. This flow makes up what is called the base flow of a stream -- the flow of a stream during dry periods of time. This flow also continue during the winter in areas where the soil freezes, providing some evidence that the majority of this water comes from the deeper aquifer rather than from the soil.
In our model, which is based in part on an actual watershed, the base flow is set to 7200 m3/hr, so the sum of the discharge flows from soil and ground water is set to be 7200 m3/hr. 95% of this flow comes from the groundwater and the remaining 5% comes from the soil. Both of these flows are defined as typical draining processes, where the rate of flow is defined as the amount in the reservoir times a rate constant. The rate constant itself is simply the base flow (multiplied by 0.95 or 0.05) divided by the initial amount in the reservoir.
Runoff
When rain falls on the surface at a high enough rate (exceeding the infiltration rate), it accumulates and forms a thin film of water that is then capable of flowing off over the surface. The rate at which it runs off of the surface and joins a flowing stream is a function of a variety of factors; the surface slope, the roughness of the surface, the thickness of water in the layer, and the average distance is has to travel to get to a stream. The roughness of the surface varies greatly, being high for densely vegetated surfaces like a prairie and low for a surface like a paved parking lot. The travel distance is related to the density of the drainage network -- the higher the density, the shorter the distance.
Here, we will define the runoff flow as another simple draining process, in which the rate constant, called k_Runoff, reflects the combined effects of the factors mentioned above.
Streamflow
Streamflow is equivalent to the volumetric rate of water flow at the downstream end of our watershed. The streamflow varies according to factors mentioned above -- the slope or gradient of the stream, the channel shape, and the roughness of the stream bed. In our model, we define streamflow as a draining process in which the volumetric rate is a function of how much water is in the river channel, but this may not be strictly true. When a stream tops its banks and spills out over the floodplain, the water is spread thinly out over a broad surface that is often vegetated (or occupied by building). The floodplain is a high-friction surface that causes the water to slow down. This means that once the river tops its banks, the rate constant ought to decrease somewhat, which will have the tendency of prolonging the flood and causing a higher flood crest.
The above processes and reservoirs are assembled into a STELLA model as shown in the figure below.
The equations used in this model are given below. Note that this model does not have a steady state to begin with. With no rainfall, the system cannot be in a steady state, and it seems odd to have a tiny, steady background rainfall to get the model into a steady state. By setting rainfall to zero, you can see what happens -- the groundwater reservoir declines, as does the soil reservoir, and the river also drops, but quite slowly.
Equations for Watershed Model
Time Unit = 1 Hour; DT = 0.25; Euler Method of
integration
Testing the Model
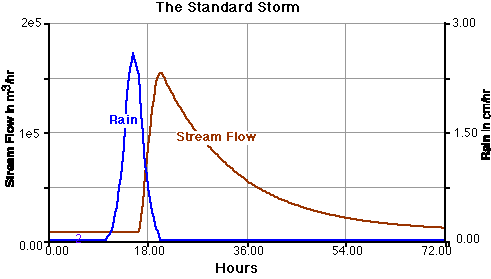
Since the model described in the equations above is not in a steady state, you can test to see if you have constructed the model properly by comparing its output with the graphs shown below for what we will call the "standard storm". Run for 72 hours with a time step of 0.25 using Euler's method of integration and plot streamflow and rain to make sure your model results are the same as the graph below.
For comparison, here is an actual hydrograph of a stream that experienced a storm.
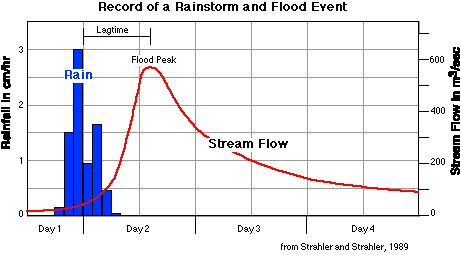
The real example is in many ways similar to our model result, indicating that our model does a reasonable job of simulating the general behavior of a real watershed system. Some of the key features to note here are that the peak stream flow lags behind the peak rainfall by some period, and the stream flow rises rapidly and then subsides more gradually, approximately following an exponential curve.
Experiments
1. Changing the Sizes of the Soil and Groundwater Reservoirs
Using the standard storm rainfall, set up a sensitivity analysis in which you change the thickness of the soil layer from 1 to 2 to 3 m for a total of three runs of the model and then make a comparative graph plotting the streamflow for each run. You may decide that in order to explain what has happened, to test an idea, you'll need to plot and study some of the other model parameters. Do the same thing with the groundwater reservoir, altering its size by changing its thickness. In our model watershed, a greater thickness of the aquifer effectively corresponds to greater topographic relief in the watershed, which would also effect the rates of flow within the groundwater, but we will leave that effect out at this stage. Summarize the effects of these changes and comment on whether or not you have changed the response time of the system.
2. Changing Vegetation of the Watershed Surface
Alter the k_Runoff parameter to simulate the effect of varying amounts of vegetative cover. For this experiment set up a sensitivity run, with an ad hoc distribution of k_Runoff varying from 0.01 to 0.1 to 1.0 for a total of three runs and plot in a comparative graph the stream flow that results from the standard rain storm specified above. A dense vegetative cover would correspond to a lower k_Runoff value, and a denuded surface would correspond to a higher k_Runoff value. Note that here, we are not changing anything about the soil properties, so this is not a simulation something like paving a watershed. Summarize the effects of these changes and comment on whether or not you have changed the response time of the system
3. Paving the Watershed
This experiment addresses a problem that faces many urban watersheds, where increased development means covering more of the land surface with an impermeable layer of asphalt, concrete, or buildings. The first change to make here is in the runoff parameter -- let's change it to 1.0 to represent a smoother, less-vegetated surface. The next change will involve the infiltration part of the model. One way to do this is to change the F_Infiltration graph such that the value is 2.0 on the left-hand side of the graph, and 0.0 on the right, following the same general form of the pre-existing graph. Before running the model, predict how the model's response will differ from the first experiment in which we only changed the k_Runoff. Study the results and comment on the changes in the lagtime and the peak magnitude of the flood as a consequence of making these changes.
4. Different Storms
The response of watershed systems to storms is sensitive to the nature of the storm -- whether it is abrupt or spread out over a longer time with uniform rainfall intensities. Our standard storm deposits about 10.5 cm of rain in the watershed, over a period of 10 hours. Let's investigate what happens if we concentrate that same amount of rain into shorter and longer time periods. To do this, insert the following input-output pairs of values into the Rain graphical converter: Brief Storm -- (10.0, 0.00), (10.2, 1.00), (10.4, 3.00), (10.6, 7.50), (10.8, 9.45), (11.0, 9.90), (11.2, 9.45), (11.4, 7.50), (11.6, 3.00), (11.8, 1.00), (12.0, 0.00). In these pairs, the first number is the time input and the second is the rainfall output. Then, for a longer, gentler storm with still approximately the same total rainfall, insert the following: Long Storm -- (10.0, 0.00), (13.0, 0.38), (16.0, 0.38), (19.0, 0.38), (22.0, 0.38), (25.0, 0.38), (28.0, 0.38), (31.0, 0.38), (34.0, 0.38), (37.0, 0.38), (40.0, 0.00). Explain the very different results caused by these different rainfall events.