Einstein's quote that "a model should be as simple as possible and
yet no simpler" makes a good sound bite, but it does not give us too
much guidance in figuring out what is simple enough and what is too
simple. This is clearly an important concept and we will examine
three versions of the familiar water tub model to illustrate varying
levels of simplicity.
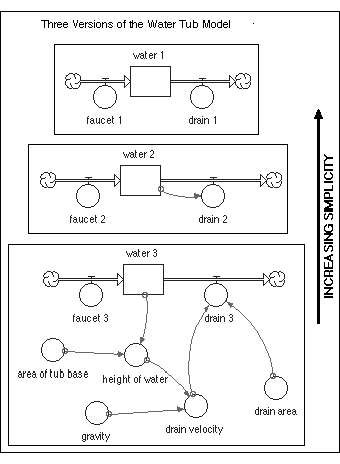
These three models are shown in Figure 2.20. The first is the
simplest, consisting of a reservoir with an inflow and outflow that
are both defined as constants - they are unaffected by the amount of
water in the tub. The second model is the one we experimented with in
the earlier part of this chapter; the inflow is a constant and the
outflow is a function of the amount of water in the tub. The third
model is the most complex and the most realistic.

Figure 2.20. Three variations on
the bathtub theme, spanning the range from greatly simplified to a
more physically realistic model based on Torricelli's Law.
It turns out that an Italian named Torricelli has examined the dynamics of this water tub system (this is the same person who invented the barometer) and after a good deal of experimentation, he came up with a general relationship that is called Torricelli's Law. This law says that the velocity of water flowing out of a drain is equal to the square root of two times gravity times the height of the water:
![]()
where v is velocity, g is gravity, and h is height. This velocity
has units of m/sec and when multiplied by the area of the drain
opening, gives an outflow in m3/sec. The
details of this calculation are shown in Figure 2.21, in which our
bathtub is replaced with a simple cylinder.
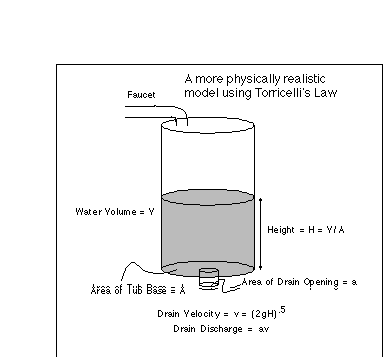
Figure 2.21. Diagram illustrating
Torricelli's Law, used to calculate the velocity and flow rate, or
discharge, from a drain at the bottom of a tub of water.
These three models thus cover a range of possibilities but even
the most sophisticated one ignores things like friction and water
viscosity and density that certainly operate in the real world. In
most cases, these additional factors are minor in comparison with the
ones represented in the model, so they do not present a serious
shortcoming of the model.
Figure 2.22 shows the results of running these three models. I set
the two more complex models up so that they have the same initial
amounts and the same steady state amounts to provide a better
comparison. As you might have guessed, this was not possible for the
simplest model.
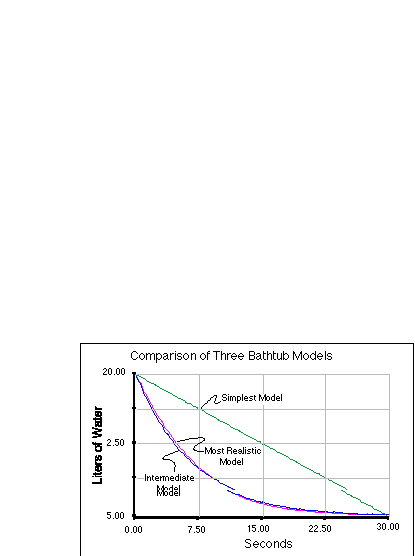
Figure 2.22. Comparison of the
three versions of the bathtub model ranging from a realistic to a
highly simplified model. Note that the intermediate model shows
virtually the same behavior as the more realistic model.
From the results, it is clear that the simplest model does a poor
job of representing the real behavior of this system; it drops off at
a constant rate and does not achieve a steady state except in the
special case where the inflow is set equal to the outflow. This
simple system does not have any negative feedback associated with it
either. So, this is a good example of a model that is too simple.
Next, let's assume that our most complex model, based on Torricelli's
Law is a nearly perfect model in that it can accurately reproduce the
results of a real system (it would be a good exercise to test this
hypothesis). The question then is whether our second model, the
intermediate one, is simple enough and yet not too simple. from the
results, it is clear that this model is nearly indistinguishable from
the most realistic model. It is similar to the best model in the
reservoir changes rapidly at first and then very slowly approaches
its steady state value - it follows an exponential curve in other
words. It also contains negative feedback, so it responds to changes
the same way that the best model does. Because of these similarities
in behavior, this second model represents a reasonable
simplification. It is qualitatively acceptable, but not necessarily
quantitatively acceptable (though in this case, the numbers are
certainly acceptable). It is simple enough and yet not too
simple.
RETURN TO MAIN PAGE