Let's explore this concept of response time in just a bit more
detail, by looking at a system where there are two drains instead of
just one. This change is easy to make. Just create another flow
starting inside the reservoir and ending outside, in another cloud
symbol and draw a connector from the reservoir to this second drain,
which we will call drain 2. To make things simple, let's pretend that
we install a new drain that is just like the original, so that it
will have the same rate constant, k=0.1. As always, try to predict
how this change will affect the system. By this point, you may be
developing a sense for how this particular system will behave, so you
may be able to predict that in general, adding another drain will
make the system respond faster to some change. But I bet you can't
predict how much faster! If you run this new model and then compare
the results to the original, you ought to see the same results shown
in Figure 2.9.
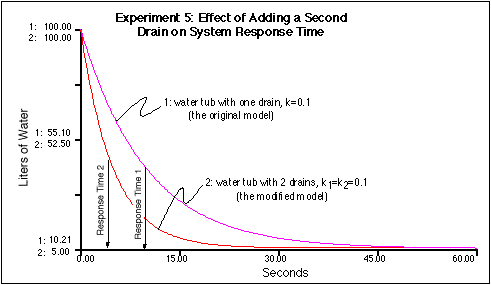Figure
2.9. Adding a second drain increases the response time. For the
modified system, the response time is 5 seconds, compared to 10
seconds for the original system. This change also alters the steady
state value for the reservoir, dropping it to 5 liters.
If you study the results of this last experiment, you can see that
in the modified model:
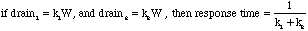
The important conclusion from this experiment is that with more outflows of the type described here, a reservoir becomes more responsive - it reacts more quickly. This modified system also present an opportunity to apply the concept of the steady state in order to answer the question of what is the steady state reservoir value for the modified system - the one with two drains. If we recall that at steady state, the inflows equal the outflows, we can make a simple equation that shows us what the steady state value must be:
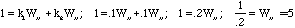
So when the water tub has 5 liters in it, the inflow of 1 liter per second will match the sum of the two outflows and the system will be in a steady state.