Alpine glaciers occur throughout the world in mountainous regions of high elevation where there is sufficient precipitation and the temperature is below freezing for much of the year.  As snow is buried under more snow, it undergoes a transformation into ice and when the ice becomes thick enough, it begins to flow, moving down a valley.  As the ice flows slowly to lower elevations, it encounters warmer and warmer temperatures until it reaches a region where there is more melting (also called ablation by glaciologists) than accumulation of ice.  These alpine glaciers may be many kilometers long, but only hundreds of meters thick, and narrow (across the valley axis) relative to their length.

Aletsch Glacier (Bernese Alps, Switzerland), is the largest glacier in the Alps.  The ablation zone in the foreground has dark stripes called medial moraines formed by the confluence of tributary glaciers further up the valley.  The whiter accumulation zone can be seen in the distance, above the red dashed lines.  Source: http://en.wikipedia.org/wiki/File:Grosser_Aletschgletscher_3178.JPG

Alpine glaciers around the world are shrinking, and many experts consider this to be like the canary in the coal mine — a warning that something is amiss.  In this case, a rapid rise in temperatures around the globe is the suspected culprit.  But, these glaciers are dynamic systems that respond to a variety of factors, and so it is important to understand how these systems work in order to understand what their decline means.

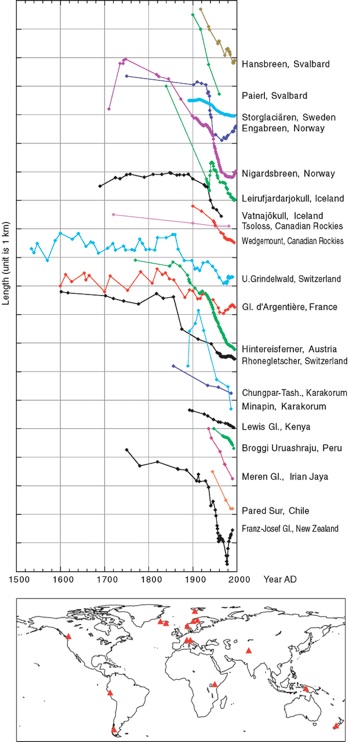
Glacier length records from different parts of the world; curves are translated along the vertical axis to make them fit in one frame.   Note that in general, there is a dramatic retreat that begins around 1900.  The Franz Josef glacier in NZ is now advancing rapidly, but its overall mass is shrinking nonetheless. Glacier locations indicated by triangles. Data are from the World Glacier Monitoring Service (http://www.geo.unizh.ch/wgms/) ; figure is from the IPCC.

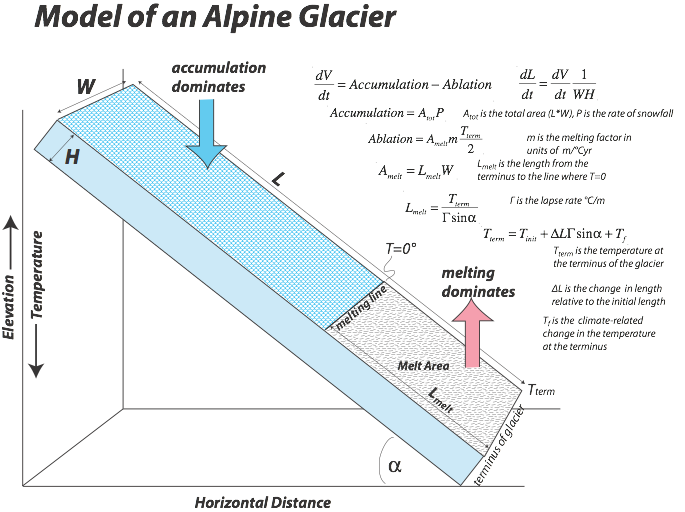
The model developed here is based on a paper by Gerard Roe, from the University of Washington, and the basics of the model are illustrated below.  The glacier is treated as a slab of ice with width W, thickness H, and length L; multiplied together these give the volume of the glacier, and W*L gives the surface area A.

The change in volume of the glacier is given by the difference between the accumulation and the ablation.  The accumulation is the total area times the rate of snowfall, while the ablation is the product of the melt area, the melting factor (whose units are in m/yr per °C) and half the temperature at the terminus of the glacier.  Why one half this temperature at the terminus?  It is because that gives an average temperature for the melt zone, since the upper limit of the melt zone is defined by the place where the temperature is 0°C.  The melt area is the width times the length of the melt area, which is given by the temperature at the terminus divided by the lapse rate (Γ) times the slope (α).  The lapse rate is simply the rate at which temperature decreases with increasing elevation.

The temperature at the terminus of the glacier is given by the initial temperature (which we must assign) plus the change in length since the beginning times the slope times the lapse rate plus any climate-related temperature change (Tf below)

Let’s think about how this system might work.  If you start out with a relatively cold temperature at the terminus of the glacier, then your ablation area might be quite small and so accumulation might dominate the ablation.  In this case, the volume of the glacier will increase, and so will its length.  This increase in length will force the temperature at the terminus to be higher (it gets warmer as you move to lower elevations); this will make a small increase in the area of ablation, and so in the next increment of time, the glacier might not advance as much.  Eventually, its advance will mean that the ablation matches the accumulation, and at that point, the length of the glacier will remain the same — it will be in a steady state.  Then, if we were to increase the snowfall, it would advance again until a new steady state was achieved; if we raised the temperature, the glacier would retreat until the ablation area shrank enough to get to a new steady state.

Basically, this system is one that will naturally try to find a steady state and it gets pushed and pulled by temperature changes and precipitation changes.  But, as we will see, it is sluggish to respond, which means that short-term temperature and precipitation changes do not have a big influence, the the longer-term changes do have a big influence.  You could even think of the glacier as a sort of filter that removes the effects of these short-term changes (many of which are essentially random noise in the climate system) and instead highlights the longer term changes.