|
Be very, very careful what you put into that head, because you will never, ever get it out. Thomas Cardinal Wolsey (1471-1530) |
 |
|
 |
Bad Coriolis FAQ | |
|
Click on the symbol for its explanation. |
||
Preamble
This FAQ (Frequently Asked Questions) is written by Alistair B. Fraser. It is in response to questions posed over the years by readers of the Bad Meteorology pages. If you have arived on this page without having read those pages or the other Bad Science pages, then what follows, will probably make little sense.Issues discussed below (arising out of the Bad Coriolis page)
Although the questions presented here are often ones asked by a specific person, each is chosen to characterize a group of similar questions which have been asked about the topic.
You have it backwards
Questions arising out of Bad Coriolis:
You have it backwards
Recently I came across your "Bad Coriolis" Web page, which I read with great interest. It seems to me that it contains an important mistake, being that the Coriolis force causes clockwise spins in the northern hemisphere and counterclockwise in the southern (your Web page states the opposite). This is to be found in any university physics textbook.
It is correct that the Coriolis force causes a moving object to experience a force to the right (left) of its path in the northern (southern) hemisphere. It is not correct that this necessarily produces a clockwise rotation. The direction of rotation (if any at all) depends upon the net force, not just a single force.
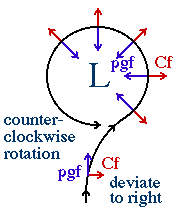
One must distinguish between the direction of deviation caused by the Coriolis force (operating on its own) and the direction of rotation (when other forces are present). Both directions of rotation are evident in both hemispheres depending upon the whether the flow is around a high pressure area (the pressure gradient force points radially outward) or around a low (the pressure gradient force points radially inward).In a geophysical flow, such as motion in the atmosphere or oceans, there is always some other force operating (such as the pressure gradient force) or how else would the material have started to move.
The illustration at the right shows a situation for a northern hemisphere low. The Coriolis force (Cf) does indeed point to the right of the flow. But it is slightly over balanced by the pressure gradient force (pgf) which points toward the center of the low (the imbalance is what causes the fluid to move along a curved path).
A good way to convince yourself of this behavior is to watch the direction of rotation seen in radar and satellite loops of storms. It is very easy to see the counterclockwise rotation around the low pressure areas in the (northern) hemisphere storms.
Excellent Site!!! Just one question re. the coriolis effect (or non-effect). I can understand that the direction of spin is dictated by local effects (shape of sink etc). But why does the water spin at all ?
If there is any motion of the water at all (say from filling or washing), and the container has walls (which is inherent in the meaning of the word container), then there must be rotary motion. After all, as a fluid parcel moves toward a wall it will be deflected and turn. It is this rotary motion which is accentuated when the water converges toward the drain. The popular illustration of this is that of the skater who spins faster as outstretched arms are brought in close to the body; the scientific explanation involves a discussion of the conservation of angular momentum.
Coriolis force? Don’t you mean coriolis effect? Pot/kettle/black?
No, I don’t mean the Coriolis effect. While one can use the word, effect, in almost any context for something which happens, I am referring to the Coriolis force. The modern convention (nearly a century old now) is that there are no preferred coordinate systems and that once you adopt a coordinate system, one gets a set of forces along with it. When you shift coordinate systems, some forces vanish, others appear. In an inertial coordinate system, there is no Coriolis force. In a rotating coordinate system there is.
No, in a rotating coordinate system, there is a Coriolis force which is as real as any other force in that it causes a mass to be accelerated. (When was the last time you saw Newton’s law say that an effect causes a mass to be accelerated?)
I was taught that the Coriolis force was not a real force, but a fictitious one. The proof of this is found in the inability of the Coriolis force to do any work.
It is true that the Coriolis force does no work. Yet, the ability to do work is not a prerequisite for a force. If the Coriolis force were to be disqualified owing to its inability to do work, it would take a number of other well established forces along with it into oblivion. For example, a charged particle, such as an electron, moving in a static magnetic field has no work done on it by that field even though it experiences the magnetic force. Alas, a claim for the fictitious nature of the Coriolis force based upon its inability to do work is an ex post facto argument (one concocted to support a position arrived at for different reasons).
In class today, my teacher told us that the Coriolis force operates independently of the direction in which an object is traveling. Yet, I have seen demonstrations of the Coriolis force where someone draws a line radially across a slowly spinning turntable. That only works when the line is drawn towards or away from the center. This implies to me that the Coriolis force only works for objects traveling in a north-south direction (or, at least, for that component of the motion). How, can I convince my teacher that he is wrong about the Coriolis force being independent of the compass bearing of the moving object.
(Yes, I really did get this as a question from a student).
I cannot help you convince your teacher, because he was right. But, maybe I can help you understand why he was right.
The conceptual difficulties arise from the demonstration you witnessed. It usually takes the form of a line (pen or chalk) drawn radially on a slowly spinning turntable. Even though the track of the pen is a straight line, the trace left on the turntable is curved. So, in the inertial frame of the classroom, the track was straight, while in the rotating frame of the turntable the track is curved. There is nothing wrong with the demonstration as it stands, however it is easy to draw the wrong conclusion from it when one tries to generalize the result, as you did. The difficulty arises from the fact that it is easy to draw the line radially, but very hard to match the velocities of the turntable and pen closely enough by hand to draw a similar line tangentially. The result of this purely logistical problem involving hand-eye coordination is that it is tempting to conclude that the Coriolis force only operates when something is traveling in a north-south direction (radially on the Earth). Incidentally, the conceptual difficulties here are similar to those experienced by the teacher in the discussion, below, about firing a missile in a northerly or southerly direction.
There are a number of ways to gain an understanding of why the magnitude of the Coriolis force is independent of the direction in which an object is traveling. I can think of (at least) three (not mutually exclusive) approaches.
1) If you reach the point where you can work through and understand the mathematics describing the force, it becomes clear that the direction of motion of the object is irrelevant; indeed, it does not even enter the equations.
2) The second approach relies upon the turntable demonstration, but applies a bit of abstract thinking to show that the result is actually far more general than it would appear to be at first blush. First one recognizes an equivalency between standing anywhere on a rotating platform (such as either the Earth or the turntable) and standing in the center of rotation. If you are standing some distance from the center, you may have thought of yourself as rotating about that distant center. But, your motion is equivalent to that of a translation and a rotation about the point at which you are standing. With this in mind, it is clear that no matter where you are, you are at the center of your own rotation. So, any movement you make over the surface is one in which you are traveling radially with respect to your own rotation center. But, traveling radially on a rotating platform was just what the turntable demonstration handled well. The trick then, is to realize that no matter in what direction you travel (say on the Earth) that you are traveling radially from the center of your own rotation (the concomitant translation component of the Earth or turntable is irrelevant) and as such your experience with what happens with the line drawn on the demonstration turntable is applicable.
3) The second approach (above) is better for students who can easily make and apply abstractions than it is is for those who cannot. So, I have built a Java visualization of the Coriolis force (and centrifugal force) which runs on the web (well, I coded up the original version, but my son rendered it into Java for me so that it would run on the web). It enables me to click anywhere and so start an object moving (green dots) over a rotating surface. Like the turntable with the line drawn by pen or chalk, this leaves a trail of footprints (red circles) which reveals the path on the turntable. But unlike the physical turntable usually used in classroom demonstrations, I can click anywhere and watch the behavior. Consequently, the student can watch as the trail moves tangentially (along a line of latitude). Further, as it is available on the web, the student can play with it him (her) -self to get an intuitive feeling for the behavior. Even better, there are controls which enable one to display the behavior in both hemispheres and even to turn various forces on and off. This maybe all well and good, but if you tried clicking on the (gif) illustration to the right and discovered that it goes nowhere, you can easily come to the conclusion that it is irrelevant if I can use a computer in class (and students can outside of class), if you do not also have access to it. Well, give me time; I will make it available to others soon, but I have run out of time this morning. Sigh...
In practice, I use all three approaches to help give my students an intuitive feeling for why the magnitude of the Coriolis force on an object is independent of the direction in which that object is traveling.
As a secondary-school Earth Science teacher, I teach the concept [of Coriolis] using the missile fired north and landing east of it’s target, and the return salvo fired south and landing west of it’s target - explaining the miss as a result of different eastward components of motion (due to Earth’s rotation) at different latitudes. Am I on solid ground here?
Whether you are on solid ground here, or not, depends in part on how you handle the issue. Does the student believe that you are explaining why there is a Coriolis force, or merely giving an example of it. There is a difference.
As an example, your illustration is not bad, but it is sufficiently restrictive as to mislead the student into believing some things which are not true. For example, the student will probably be prompted to believe, as a result of this illustration, that:
- 1) the Coriolis force only operates on objects traveling in a north-south direction (indeed, I have seen web pages which offer this false claim); and
- 2) it really is the latitudinal differences in easterly component which causes the behavior (while, in fact it is not).
Alas, neither of these is true. (A cat may be an example of an animal, but that does not mean that to be an animal, one must be a cat).
In fact, the magnitude of the Coriolis force is independent of the direction in which something is moving. If you were to present your example as if it were an explanation of the Coriolis force, you are now stuck with its inability to handle the behavior of a missile as it goes similarly off track after being fired in an easterly or westerly direction.
But, there are pedagogical shoals to navigate here even if you are very careful to tell your students that you were not explaining the Coriolis force but merely giving an example of its behavior in a highly restricted situation: they are unlikely to believe you, or at least, not to understand the distinction you are making. They will take your description of the elephant’s leg and assume that the whole beast is topographically equivalent to a tree trunk. Of course, students can be forgiven for failing to understand the difference between an example and an explanation, because so many teachers also fail to understand the distinction. Sigh....
I use the difference in the size of hurricanes and sinks to explain to students why the Coriolis force affects the one and not the other. Thus, I note that there is a much bigger difference in the underlying easterly component of the earth’s velocity as one goes from the north side of a hurricane to its south side than there is if one goes from the north side of a sink to its south side. Yet, on your page, you stress that the differences in behavior result from differences in time, not space. Am I off base?
Explanations are funny things. Indeed, what do you mean by suggesting that the difference in behavior is a result of the difference in the (underlying) velocity. Let’s start by ignoring the fact that you thought (incorrectly) that the issue was just the easterly component of the velocity and just explore the difference between these two situations: the large scale with a big velocity difference and the small scale with a small velocity difference. The implication is that if one were to match the velocity differences on the two scales, then the Coriolis force, or maybe the displacement, would suddenly be the same in each case. Alas, it would not be so (unless other things were also fudged).
The traditional response to what you have suggested is that you have confused two things, a spatial scale and temporal scale. As usually presented, the Coriolis force (being a force) produces a result (such as displacement) over time. The spatial scale (how far it is across something, or how far an object travels) does not even appear in the equations. There is much to commend this approach. Within this context, it is not the spatial scale that produces the effect (for a given force), but how long the event lasts. A sink drains quickly (not much time for a small force to produce a significant displacement); a missile or the air in a hurricane takes much longer to traverse its territory (a much longer time for a force to produce a significant displacement).
Of course, any expression can be transformed into any related variable, so it is legitimate (although not conventional) to express the lateral displacement resulting from the Coriolis force as a function of the change in velocity of the (underlying) reference system (such as the latitudinal variation in the tangential velocity of the Earth’s surface). But, when one puts the expression in terms of the velocity difference across the region, other variables pop up, and one discovers that such an approach moves one further away from a simple understanding what is going on, rather than closer to it.
So, I recommend that in your class, you not use the argument about the latitudinal variation of the Earth’s tangential velocity. The first reason is that it cannot (intuitively) account for the Coriolis force when an object is traveling along a line of latitude (see, on firing missiles, above). The second reason is that it misleads the students into believing that it really is the velocity difference across the region that accounts for the difference in behavior between hurricanes and sinks.
Bizarre ideas readers report that they have seen apparently being seriously attributed to the Earth’s rotation. (The incredible is fodder for the credulous).
