Notice that in both cases shown in Figure 2.6, the system returns
to the steady state in the same amount of time. Now, try to predict
what will happen if we get a bit more extreme and put 100 liters in
the bathtub to begin with. Do you think the system will recover and
return to its steady state in the same amount of time? My initial
impulse is to say that it will take longer, but I know that dynamic
systems can be difficult to predict, so I am not confident in this
intuitive prediction. Think about this carefully, and then do an
experiment where you alter the initial conditions so that the tub
starts out with 100 liters and run the model. If you compare the
results with those shown in Figure 2.6 above, you will see that in
fact, the system does return to the steady state in the same amount
of time - quite a surprise. Let's investigate this a bit further and
at the same time learn about a powerful feature of the program -
sensitivity analysis.
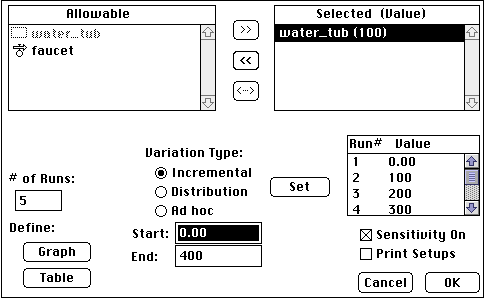
Select Sensi Specs from the Run menu; this brings up a window that
allows to set a sensitivity analysis, where you systematically change
one parameter in a uniform way and monitor the system's response.
Click on water tub in the Allowable column and send it over to the
Selected column by pressing the >> button. Then click on water
tub in the selected column to highlight it; enter 5 in the box titled
# of Runs, make sure that the Incremental button is highlighted, then
set the beginning and ending values of water tub at 0 and 400. When
you've done this, a list of the initial values for the water tub
reservoir will appear in the column on the right. Click the box next
to Sensitivity On, you are ready to go. Consult Figure 2.7 to make
sure you've entered the right values in the right places in the
window before proceeding. If you have troubles here, consult the
STELLA manual.

Figure 2.7. The sensitivity
window in STELLA, used to systematically change on part of the
system. You may either click on the Define Graph button in this
window, or you can alter a pre-existing graph so that it plots all
five sensitivity runs by making sure that the Comparative button is
highlighted in the Define Graph window.
Make sure that your graph is set up to plot all of the sensitivity
runs; the comparative button must be checked in the Define Graph
window. Then, as you select S-Run from the Run menu, the program will
cycle through five simulations, each with a different starting value
for the reservoir. Your ending graph should look like Figure 2.8
below.
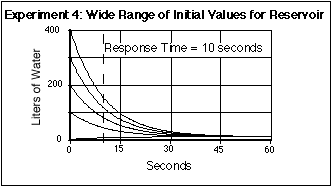
Figure 2.8. With a variety of
initial values for the reservoir, the system returns to the steady
state in which the reservoir has a value of 10 liters in the same
amount of time. The response time is independent of the initial value
of the reservoir; instead, it is defined as 1/k where k in our case
is 0.1 seconds-1. Thus the response time here
is 10 seconds, shown by the vertical dashed line.
Sure enough, we see that the time it takes to return to steady state is completely independent of the amount of water initially in the water tub. Notice that the approach to the steady state value follows what is called an exponential curve -its slope is constantly changing and as it approaches its ending value, the curve changes very slowly. This makes it a little difficult to say just when the system has returned to its steady state. For this reason, it is convenient to define the response time a bit differently. If we say that the outflow process, the drain, is defined as a rate constant, k, times the amount in the reservoir, W, then the response time is defined as:
![]()
In our case, k is 0.1 and the units are /second, so the response
time is 10 seconds. Another way of saying this is that the response
time is the time at which the initial imbalance in the system, the
difference between the initial value and the steady state value for
the reservoir, has been reduced by 63%. With this relationship
defined, we can accurately predict the effect of changing the
parameter k from 0.1 to 0.5; it will reduce the response time to 2
seconds instead of 10. This concept of a response time is an
important one - it will help you develop a better intuitive sense for
how a system will behave.
RETURN TO MAIN PAGE